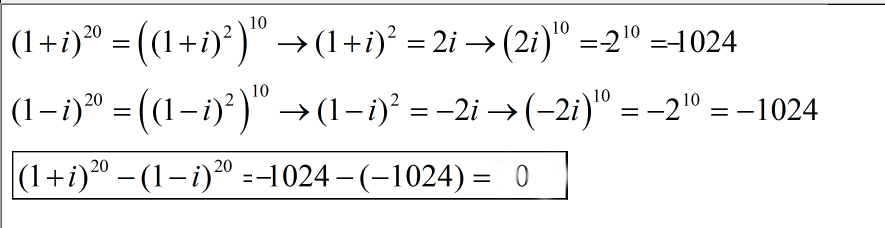-
Hola,
he estado haciendo estos ejercicios y no obtengo los mismos resultados que la solución dada...quisiera saber si me he confundido yo o no
Mi solución:
A) (-infinito,-5] U [5,infinito) corchetes en -5 y 5, no paréntesis
B) Coincide mi respuesta
C)Coincide mi respuesta
D) [3,infinito)
E) Coincide mi respuesta
Saludos
-

Ángel
el 14/10/16PROBLEMA: [(x+1/x^2-4):(x+1/x+2)] + [(2x-4/x):(x-2)]
1º) Efectuamos las divisiones de dentro de los paréntesis ("multiplicamos en cruz")
[(x+1)(x+2)/(x^2-4)(x+1)] + [2x-4:((x)(x-2))]
2º) Simplificamos
[(x+2)/(x^2-4)] + [(2x-4)/(x^2-2x)]
3º) Pasamos a común denominador ambas fracciones
[(x+2)(x^2-2x):(x^2-4)(x^2-2x)] + [(2x-4)(x^2-4):(x^2-2x)(x^2-4)]
4º) Sumamos ambas fraciones para que nos dé un solo término
(x^3-2x^2+2x^2-4x+2x^3-8x-4x^2+16)/(x^4-2x^3-4x^2+8x)
5º) Simplificamos
SOLUCIÓN: (3x^3-4x^2-12x+16)/(x^4-2x^3-4x^2+8x)
**Para comprobar que el problema de origen es equivalente a nuestra solución comprobamos sustituyendo la "x" por un valor al azar y tenemos que obtener lo mismo.
Por ejemplo, con x=3, el resultado al sustituirla en el PROBLEMA y la SOLUCIÓN es 5/3
-


Antonio Silvio Palmitano
el 14/10/16Debes corregir.
Primero, expresemos a los números complejos en forma polar (módulo y argumento).
z1 = 1 + i (observa que está representado por un punto en el primer cuadrante):
Módulo: V(1^2 + 1^2) = V(2)
tangente de su argumento: tanA = 1/1 = 1, argumento: A = arctan(1) = 45°
luego, el número expresado en forma polar queda: z1 = (V(2))(45°), luego pasamos a su potencia:
z1^20 = ( (V(2))(45°) )^20 = fórmula de De Moivre para potencias = ( (V(2))^20 )(20*45°) = (2^10)(900°) = (1024)(180°), luego pasamos a forma trigonométrica:
z1^20 = 1024*(cos180° + i*sen180°) = reemplazamos valores = 1024*(-1 + 0i) = -1024.
Luego hacemos lo propio con el segundo número complejo:
z2 = 1 - i (observa que está representado por un punto en el cuarto cuadrante):
Módulo: V(1^2 + (-1)^2) = V(2)
tangente de su argumento: tanA = -1/1 = -1, argumento: A = arctan(1) = 315°
luego, el número expresado en forma polar queda: z1 = (V(2))(315°), luego pasamos a su potencia:
z1^20 = ( (V(2))(45°) )^20 = fórmula de De Moivre para potencias = ( (V(2))^20 )(20*315°) = (2^10)(6300°) = (1024)(180°)
(observa que 6300°/360° = 17,5 giros = 17 giros + 0,5 giro, que es equivalente a: 0,5*360°= 180°),
luego pasamos a forma trigonométrica:
z2^20 = 1024*(cos180° + i*sen180°) = reemplazamos valores = 1024*(-1 + 0i) = -1024.
Luego efectuamos el cálculo:
z1^20 - z2^20 = -1024 - (-1024) = -1024 + 1024 = 0.
Te sugiero mires los vídeos sobre números complejos.
Y para resolverlo en forma binómica, seguimos el planteo del colega César:
(1+i)^20 = ( (1+i)^2 )^10 = (1 + 2i + i^2)^10 = (1 + 2i - 1)^10 = (2i)^10 =
= 2^10 * i^10 = 1024 * ( i^2)^5 = 1024*(-1)^5 = 1024*(-1) = - 1024;
(1-i)^20 = ( (1-i)^2 )^10 = (1 - 2i + i^2)^10 = (1 - 2i - 1)^10 = (-2i)^10 =
= (-2)^10 * i^10 = 1024 *( i^2)^5 = 1024*(-1)^5 = 1024*(-1) = - 1024.
Luego restamos, y el resultado es cero.
Espero haberte ayudado.
-
hola, tengo una duda sobre algebra lineal, me podrian explicar de donde se deduce esto, sea B base ortonormal= {v1, v2..., vn} y el vector W se cumple que : W= <w.v1>v1 + <w.v2>v2+..+<w.vn>vn
-


Antonio Silvio Palmitano
el 13/10/16Podemos comenzar por multiplicar y dividir por la expresión "conjugada" del numerador y queda (llamamos N al numerador y D al denominador):
N = (V(ax + b) - 2)(V(ax + b) + 2) = (V(ax + b))^2 - 2^2 = ax + b - 4, y observa que N tiende a (b - 4) cuando x tiende a 0.
D = x(V(ax + b) + 2), y observa que D tiende a 0 cuando x tiende a 0.
Luego, para que el límite de la expresión fraccionaria exista debemos imponer que N tienda a 0, por lo que tenemos: b = 4, y la expresión fraccionaria queda:
N/D = ax / ( x(V(ax + 4) + 2) ) = simplificamos = a / (V(ax + 4) + 2), y observa que la expresión tiende a a/4 cuando x tiende a 0, por lo tanto tenemos: a/4 = 1, de donde tenemos: a = 4.
Luego, la expresión fraccionaria queda:
N/D = ( V(4x + 4) - 2)/x = ( V(4(x + 1)) - 2 )/x = (2V(x + 1) - 2)/x = 2(V(x + 1) - 1)/x.
Espero haberte ayudado.
-
Buenas noches, quería que me ayudasen a despejar la X en esta ecuación matricial, ya que hay una AX y un 3X y no sé si se puede operar con ellos, ya que la X está en posiciones distintas. Gracias.



Nico
el 13/10/16Hola Victor, planteate una matriz genérica, multiplicala y sumala con las demas matrices tal cual te lo indica la ecuacion, al final te quedara una matriz de cada lado del = y simplemente tenes que resolver el sistema igualando entrada a entrada
Si no te queda claro házmelo saber..
Saludos!
-
como tengo que hacer para resolver senx= cosx ?


Antonio Silvio Palmitano
el 13/10/16Observa que puedes escribir:
senx = 1*cosx, luego haces pasaje de factor como divisor:
senx / cosx = 1, luego expresamos la tangente como seno sobre coseno:
tanx = 1, luego tenemos (observa que tenemos ángulos en el primer y tercer cuadrante)
x = 45° + 360° * k, con k perteneciente a Z,
x = 225° + 360° * m, con m perteneciente a Z.
Observa que los valores de x que anulan al seno o al coseno no son soluciones de la ecuación.
Espero haberte ayudado.