-
Wayner
el 13/10/16<p>Unicoos, podrian ayudarme en este ejercicio, por lo que veo este topo de ejrcicio tiene 6 solucion desde Z=0 hasta Z=5 pero ninguna de las solcuiones me da la solucion expuesta. La respuesta correcta es b) -64.</p>
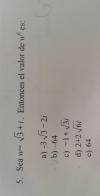
Antonio Silvio Palmitano
el 13/10/16Observa que w tiene parte real V(3), parte imaginaria 1, y que su representación corresponde a un punto en el primer cuadrante. Luego:
su módulo es |w| = V( (V(3))^2 + 1^2) = V(3 + 1) = V(4) = 2;
la tangente de su argumento es: tanA = 1/V(3), y su argumento es: A = 30°.
Luego, el número expresado en forma polar queda:
w = (2)(30°),
luego, con la fórmula de De Moivre para potencias tenemos:
w^6 = ( (2)(30°) )^6 = aplicamos la fórmula = (2^6)(6*30°) = (64)(180°),
luego, el número expresado en forma trigonométrica queda:
w = 64*(cos180° + isen180°), resolvemos y queda:
w = 64*(-1 + i*0) = - 64.
Espero haberte ayudado.
-
Angel Cencerrado Mazuecos
el 13/10/16hola soy nuevo en esto y me gustaría que pusiera un video de ecuaciones con fracciones y con raíces
gracias
-
Karla De Roa
el 13/10/16Hola necesito un favor, podran ayudarme a derivar con respecto a X y Y la siguiente derivada S= 3 sen 2X³Y², se me hace complicado entenderle aun y mas con sen y cos....
Antonio Silvio Palmitano
el 13/10/16Si la expresión es: S = 3*sen(2x^3 * y^2), podemos plantearla como composición de funciones:
S = 3*sen(u),
con u = 2x^3 * y^2, cuyas derivadas parciales son:
du/dx = 6x^2 * y^2,
du/dy = 4x^3 * y.
Luego, las derivadas parciales de la función compuesta S quedan:
dS/dx = 3*cos(u) * du/dx
dS/dy = 3*cos(u) * du/dy.
Solo queda para que sustituyas las expresiones de u, du/dx y du/dy, y terminado estará el trabajo.
Espero haberte ayudado.
-
Juan Martín Vargas
el 13/10/16Buenas, tengo una duda respecto a el crecimiento/decrecimiento de la función f(x) = x^5 + x + 1. Tomando la derivada primera se obtiene f'(x) = 5x^4 + 1, luego obtenemos las raíces planteando f'(x) = 5x^4 + 1 = 0, esta ecuación no tiene soluciones en los reales, de que forma podría obtener el crecimiento de la función? máximo y mínimo local en el intervalo [-1,1]? Gracias!
Antonius Benedictus
el 13/10/16
Antonio Silvio Palmitano
el 13/10/16Observa la expresión de la función derivada tienes el primer término que es positivo (producto de una potencia con exponente par por un número positivo) y el segundo término también es igula a 1, que es positivo, por lo que resulta que la derivada toma valores estrictamente positivos para todos los números reales, por lo que tenemos que la función es estrictamente creciente en R.
Luego, si nos restringimos al intervalo, tenemos que es cerrado, y como la función es continua, tenemos que alcanza extremos absolutos en el intervalo y, como ya hemos determinado que es estrictamente creciente, tenemos que f alcanza:
Máximo absoluto en x = 1, y f(1) = 3,
mínimo absoluto en x = -1, y f(-1) =-1.
Es muy conveniente que grafiques, a fin de visualizar mejor la situación planteada.
Espero haberte ayudado.
-
paco meirinho
el 13/10/16hola mi pregunta es la siguiente: en una prueba me pidieron que buscara el valor de X:
XCX - A3BCX= XC+A3BC , lo que me complico en el ejercicio fue el XCX que no pude despejar X, al parecer el resultado fue la identidad, pero lo hice mal por que despeje x por la derecha así :
(XC - A3BC) X=XC+ A3BC / ( XC - A3BC)-1 supuesto de que existe la inversa
X= (XC + A3BC)(XC-A3BC)-1
HASTA ACA PUDE LLEGAR POR QUE NO SE QUE ESTOY HACIENDO MAL O QUE NO SE PUEDE HACER. SALUDOS Y GRACIAS DESDE YA
Juan Martín Vargas
el 13/10/16paco meirinho
el 13/10/16
Antonius Benedictus
el 13/10/16Juan Martín Vargas
el 13/10/16paco meirinho
el 13/10/16paco meirinho
el 13/10/16SEAN LAS SIGUIENTES MATRICES:
A= 0 1 3 B = 30 20 100 C= 2 0 1
0 0 -2 4 23 30 3 1 4
0 0 0 -45 34 23 5 1 0
a) demuestre que la matriz C posee inversa
b) encuentre el valor (o los valores) de X en la ecuación
XCX - A^3BCX=XC + A^3BC
(HINT: resuelva para X, y primero obtenga el valor de A^3)
c ) resuelva det(A^30BC^-1)
-
dovigame
el 13/10/16Podrían ayudarme con este determinante lo he hecho pero el valor que obtengo a mi no me es fiable.Lo he hecho por eliminación de filas por columnas,por gauss y nada la x y la z me dan el mismo resultado 1 positivo para las dos y 1 negativo tambien
Antonio Silvio Palmitano
el 13/10/16Va una orientación:
Primero realiza operaciones elementales entre filas (se sustituye la fila nombrada primero por la resultante luego de operar):
F1 - F2
F2 - F3
F3 - F4
Luego, podrás extraer factor común en la primera fila y en la tercera fila.
Luego, realizas la operación elemental:
F4 - F1
Y verás que queda un determinante de orden 3 muy sencillo para resolver.
Espero haberte ayudado.
-
Jordi Ramos
el 13/10/16
Hola amigos necesito su ayuda con este ejercicio, no entiendo como sacar las raices me complica el coeficiente complejo
David
el 13/10/16Para hallar las racies debes averiguar cuando f(x)=0... Por tanto x³+1-√3.i=0... de donde x³=-1+√3.i.... x=³√(-1+√3.i)
Y ahora la raiz cubica de un numero complejo como en este vídeo... Numeros complejos 04 - RaizNos cuentas ¿ok?
Antonio Silvio Palmitano
el 13/10/16Planteamos la condición para raíces:
f(x) = 0, sustituimos
x^3 + 1 -V(3)i = 0, hacemos pasajes de términos:
x^3 = - 1 + V(3)i
observa que a la derecha tenemos un número cuya representación es un punto en el segundo cuadrante, luego
calculamos su módulo: |-1+V(3)i| = V(1 + 3) = V(4) = 2,
y la tangente de su argumento: tanA = V(3)/(-1) = - V(3), y luego su argumento: A = 120°,
luego expresamos al número complejo en forma polar, y la ecuación queda::
x^3 = (2)(120°), hacemos pasaje de potencia como raíz (indicamos raíz cúbica como (3V)):
x = (3V)( (2)(120°) )
luego aplicamos la fórmula de De Moivre para las raíces (recuerda que serán tres, según el Teorema Fundamental):
x = ( (3V)(2) ) ( (120° + 360°*k)/3 ), con k = 0, 1, 2.
Luego, resolvemos y tenemos las tres raíces:
x1 = ( (3V)(2) )(40°)
x2 = ( (3V)(2) )(160°)
x1 = ( (3V)(2) )(280°)
Luego puedes expresarlas en forma trigonométrica y a partir de allí en forma binómica.
Espero haberte ayudado.
-
Toby
el 13/10/16Hola
Desearía que de favor me pueda ayudar mi estimado profesor Antonio Benito García o algun otro experto o hábil, me podria explicar como puedo resolver un sistema de ecuaciones. Pero no cualquiera. En realidad lo que tengo son dudas,
Por ejemplo si sé como revolver el sistema de ecuaciones dada por x+y=5 :x-y=5
O de ecuaiones cuadraticas como y=x2 -1 : y=-x2+1
Parece que fueran casos particulares..
Pero no puedo resolver el sistema como por ejemplo..
y=senx : y=x al igualar queda x= sen x ¿Como despejo x? Senx/x=1 quizas...
O se resuelve de otro metodo. Otro sistema imposible de resolver es y=ex : y=3x+2
ln y=x ln e , esto implica que ln y= x , sustituyendo en la otra ecuación queda...
y=3(ln y)+2 ..... ¿Cómo despejo y?
¿Se me ocurrio el método gráfico? Pero el problema es que es muy tedioso o no es tan exacto?
¿Qué debo hacer, que metodo se sigue?
Ayuda, Gracias de antemano.....
David
el 13/10/16La unica opcion para resolver la ecuacion x= sen x es que representes la funcion x-senx y compruebes cuando es cero (cuando corta el eje x)...
Lo mismo para la otra ecuacion que planteas.. Pero ¿estás seguro de que te piden resolver esas ecuaciones o SOLAMENTE DEMOSTRAR QUE TIENE SOLUCION?
En este ultimo caso, solo tendrías que recurrir al TEOREMA DE BOLZANO... Teorema de BOLZANO
O TAMBIÉN Teorema de Bolzano-Rolle unica raiz de una funcion -
Deidara Stick.
el 13/10/16
+cHola. Buen día unicoos.
Les pido de favor que me ayuden con demostrando si la respuesta de la integral inmediata es correcta o incorrecta.
Les pido ayuda con esto de favor les ruego. Mil gracias de antemano. Saludos.
-
Sebástian
el 13/10/16Que tal unicoos, alguien me puede ayudar con el sgte problemade mate.
Curva: y = x + Sen (x)
○ Hallar el área límitada por la curva y el eje x si x ∈ [-10,10] . (x está dado en enteros "Z").
○ Halle la longitud de la curva desde x=-10 y x=10, es decir x ∈ [-10,10].
Esperare la ayuda, gracias de antemano, gracias y saludos equipo unicos.
David
el 13/10/16Lo primero que debes hacer es representar la función en ese intervalo para hallar los puntos de corte con el eje x...
Y despues hacer integrales definidas... Te sugiero.. Integral definida AREA de una funcionPERO.... dado que tu caso es una función impar, bastará con hacer la integral entre 0 y 10. Y luego multiplicarla por 2...
Echale un ojo a wolfram para visualizar la gráfica de tu función http://www.wolframalpha.com/widgets/view.jsp?id=21d84dfa8a9d3135d928494d888b9ece
David
el 13/10/16Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?
