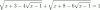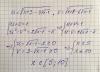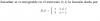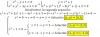-


Antonio Silvio Palmitano
el 13/10/16Llamemos: V(x - 1) = t,, de donde tenemos: x - 1 = t^2 y luego: x = t^2 + 1 (*). Sustituimos y la ecuación queda:
V( t^2+ 1 + 3 - 4t ) + V( t^2 + 1 + 8 - 6t ) = 1, reducimos términos semejantes y ordenamos términos en los argumentos de las raíces y queda:
V( t^2 - 4t + 4 ) + V( t^2 - 6t +9 ) = 1, factorizamos los argumentos de las raíces y queda:
V( (t - 2)^2 ) + V( (t - 3)^2 ) = 1, simplificamos potencias y raíces (recuerda que V(u^2) = |u|) y queda:
|t - 2| + |t - 3| = 1, luego tenemos cuatro opciones:
1) t - 2 >= 0, t - 3 >= 0, t - 2 + t - 3 = 1, que nos conduce a: t >= 2, t >= 3, t = 3, que corresponde a t = 3, y por la ecuación señalada (*) tenemos: x = 10.
2) t - 2 >= 0, t - 3 < 0, t - 2 - (t - 3) = 1, que nos conduce a: t >= 2, t < 3, 1 = 1, que nos conduce a: 2 <= t < 3, y por la ecuación señalada (*): 5 <= x < 10.
3) t - 2 < 0, t - 3>= 0, - (t - 2) + t - 3 = 1, que nos conduce a: t < 2, t >= 3, -1 = 1, que nos conduce al conjunto vacío.
4) t - 2 < 0, t - 3 < 0, - (t - 2) - (t - 3) = 1, que nos conduce a: t < 2, t < 3, t = 2, que nos conduce al conjunto vacío.
Luego, el conjunto solución escrito como intervalo queda: S = {10} u [5,10) = [5,10].
Espero haberte ayudado.
-
Buenas, necesito que me ayuden con este ejercicio:
Halla el resto de dividir M(x) = 3x^32 - 2x^12 + x^9 + x + 6 : 3/5x + 3/5 Justifica el procedimiento utilizado.
Seria de mucha ayuda, desde ya, muchas gracias...

David
el 13/10/16¿¿?? Haz la división.... Division de polinomios
También puedes intentar que el divisor sea del tipo (x-a) o (x+a) para poder aplicar el teorema del resto.. Teorema del restoMultiplica por 5 a numerador y denominador...
(15x^32 - 10x^12 + 5x^9 + 5x + 30) : (3x + 3)
Divide entre 3 a numerador y denominador...
(5x^32 - (10/3)x^12 + (5/3)x^9 + (5/3)x + 10) : (x + 1)
Y ahora, simplemente sustituye x por -1 para obtener P(-1). Ese será tu resto.. -
Hola Unicoos! Según el Teorema De Bolzano. ¿Cómo se resolvería este problema?
Sabiendo que la función f(t)=(at^5+bt^3-4)/t+1 y f(5)=12, demostrar que en algún punto del intervalo [0,5], f(t)=8
Gracias!!!!
-
Buenas unicoos, podrian.ayudarme en este ejercicio de numeros complejos: NOTA: Z debajo de una barra, es el conjugado de los numeros imaginarios z= a-bi. Y z entre dos barras, es el modulo del numero complejo: /Z/= raiz a^2 + b^2. La solucion del ejercicio es : 8i-44/10
Tengo la idea de como hacerlo pero no se por donde empezar ya quelo resolvi y no me da el resultado expuesto.



David
el 13/10/16(2-2i).(4-3i) / (4+3i-5) pues el modulo de z es √(4²+3²)=√(16+9)=√25=5...
Y ahora opera.. (8-6i-8i+6i²) / (-1+3i) = (2-14i) / (-1+3i) ....
Te sugiero.. Números complejos -
Tengo que resolver el siguiente sistema de ecuaciones mediante el método de substitución. Tengo que aislar la Y de la primera ecuación y sustituirla en la segunda.
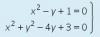


Antonio Silvio Palmitano
el 13/10/16Un camino alternativo, podría ser restar la segunda ecuación con la primera, lo haces y queda (observa que se cancelan los términos x^2):
y^2 - 3x + 2 = 0, que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y tienes:
y1 = 1, reemplazas en la primera ecuación inicial y queda: x^2 = 0, y luego: x = 0, y tienes una solución: (0,1);
y2 = 2, remplazas en la primera ecuación inicial y queda: x^2 - 1 = 0, de donde tienes: x^2 = 1, que conduce a dos opciones:
x = -1, con la que tienes otra solución: (-1,2),
x = 1, con la que tienes otra solución más: (1,2).
Espero haberte ayudado.
-
Hola buenas tardes me pueden ayudar con este problema.
Describir el cnjunto de puntos Z en el plano complejo que satisfaga la ecuacion.
Re((1+i)z+1)=0
me podrian decir como se resuerlve no entiendo que debo hacer


Antonio Silvio Palmitano
el 12/10/16Tenemos: (1+i)z + 1 =
= (1+i)(x+yi) + 1 = distribuimos:
= x + yi + xi - y + 1 = agrupamos términos:
= (x - y + 1) * (y + x)i, luego igualamos su parte real a cero y queda:
x - y + 1 = 0, luego despejamos y tenemos la ecuación cartesiana explícita:
y = x + 1, que corresponde a una recta con pendiente m = 1 y ordenada al origen b = 1.
Espero haberte ayudado.