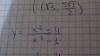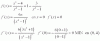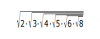-
Mireia
el 4/10/16Hola! ¿Podéis explicarme el teorema de Darboux? Sobretodo quería que hicierais algún exercicio aplicándolo porque en la teoria más o menos lo entiendo pero no lo sé aplicar. ¡Gracias con antelación!
Antonius Benedictus
el 4/10/16NATURA NON FACIT SALTUS
Esto es, la naturaleza pasa de un estado a otro atravesando todos los estados intermedios.
SI un proceso metabólico es continuo y a las 9 de la mañana hay 15 g de glucosa, pero a las 11 de la mañana solo hay 12 g, entonces durante al menos un instante entre las 9 y las 11 la cantidad de glucosa tiene que ser de 14 g (por ejemplo).
-
Matías
el 4/10/16Me ayudan con el 3?
chado
el 4/10/16solo tenes que obtener la derivada en X=0 de la funcion, ver como se comporta la funcion en el entorno e ese punto (si te da con signo positivo a la izquierda y negativo a la derecha entonces es maximo, caso inverso es minimo ), y hacer lo mismo con la derivada segunda en ese punto. si no te podes guiar con esto lo resuelvo si asi lo necesitas ;)
chado
el 4/10/16con tu funcion derivada,
ex+cos(x)-2-x
pruba un valor cercano al 0 por derecha y por izquierda, por ejemplo el -0.05 y el 0.05 en tu funcion derivada
veras como en -0.05 obtendras un valor negativo, (funcion decrece a la izquierda) y en 0.05 un valor positivo (tu funcion crece a la derecha) con esto podras decir que tiene un minimo relativo en el punto (0,0)
-
Jessica
el 4/10/16Buenas! tenia una duda en esta funcion y es como comprobar los extremos; lo he intentado en clase con otro compañero y con la profesora pero al final no sabiamos como avanzar. Gracias de antemano
-
Carla
el 4/10/16Hola, me preguntaba si podían contestar mi duda. Cómo puedo resolver esos 3 ejercicios aplicando ya sea el teorema del valor medio o de Rolle? Gracias de antemano.
-
skiler 8
el 4/10/16Hola,buenas tardes, David, o alguien,¿podria resolverme esta duda? esque mi profe de mates no explica casi nada porque dice que es muy facil y,que siempre es lo mismo y, encima de que lo poco que explcia lo explica rapido,pues... en fin,el caso esque ayer,explico una cosa nueva que se llaman las ecuaciones factorizadas y factorizables y, no estuve ese dia, asique, no se como hacerlas, porque hoy no las ha vuelto a explicar.David,¿podrias hacer un video sobre esto, porfavor? te lo agradeceria mucho o, solo responderme y decirme como se haria o, sino que otro usuario me intente resolver la duda, eso seria genial,gracias. Aqui dejo los ejemplos.¡Gracias de antemano!:
A) (3x-6)^5=0
b)4x^2(x+1)^2(x-2)=0
c) (x`2)(x^2+1)(x^2+5)=0
-
Maria del castillo
el 4/10/16
— Una fábrica de dispositivos eléctricos fabrica tres tipos de componentes a partir de
cobre y estaño:
Dispositivo A: Necesita 8 unidades de cobre y ninguna de esta˜no.
Dispositivo B: Necesita 6 unidades de cobre y 2 de esta˜no.
Dispositivo C: Necesita 7 unidades de cobre y 1 de esta˜no.
En un momento dado se disponen de 100 unidades de cobre y 12 de esta˜no,
1. ¿Cu´antas dispositivos de cada tipo se pueden fabricar usando todo el material disponible?
2. Sabiendo que el precio de producción del dispositivo A es de 2e, el de B es de 7e y el de
C es de 5e, ¿Hay alguna combinación que cueste 60e consumiendo todo el material?
3. ¿Cuáles son las cantidades máxima y mınima de euros que se pueden invertir para tener
producción de componentes con la condición de invertir todo el material de cobre y
estaño?
Alguien que me ayude a resolver este ejercicio?
David
el 6/10/16¿Y cual es tu duda?.. ¿el planteamiento? ¿la resolucion del sistema?. ¿todo?..
Programación lineal
Si es todo, te sugiero los vídeos de PROGRAMACION LINEAL y los de SISTEMAS COMPATIBLES INDETERMINADOS -
Nerea
el 4/10/16
Este ejercicio está en mi libro de matemáticas y no sé cómo hacerlo. El enunciado es el siguiente: ''escribe bajo un sólo radical y simplifica''.
¿Podríais explicarme muy facilmente cómo hacerlo?
-
Sebastian
el 4/10/16Hola buenas tardes, me podrían ayudar con el siguiente determinante? Lo máximo que llegue a hacer es uno de 4x4 por sarrus y este no se si se hace igual o se podría hacer por otro método. Muchas gracias
-
Antonio
el 4/10/16Alguien me ayuda con el siguiente ejercicio? Es demostrar por induccion completa lo siguiente:
Antonius Benedictus
el 4/10/16
Antonio Silvio Palmitano
el 5/10/16Proponemos la solución: (u)n = c*r^n, con c perteneciente al conjunto de los números reales.
Reemplazamos en la fórmula recursiva y queda:
c*r^n = c*r^(n-1) + 2*c*r^(n-2)
Dividimos en todos los términos por c*r^(n-2) y queda:
r^2 = r + 2, hacemos pasaje de términos y queda:
r^2 - r - 2 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
r1 = 2, r2 = -1
Luego, el elemento general que proponemos queda:
(u)n = c*2^n + d*(-1)^n (*),
en la que c y d son constantes a determinar.
Luego, planteamos los dos primeros elementos, cuyos valores tenemos como datos en el enunciado:
Para (u)0:
c + d = 2
Para (u)1:
2c - d = 7.
Luego resolvemos el sistema de ecuaciones y su solución queda: c = 3, d = -1.
Luego, la expresión del elemento general de la sucesión la obtenemos reemplazando en la expresión señalada (*)
(u)n = 3*2^n + (-1)*(-1)^n,
resolvemos en el segundo término, y llegamos a
(u)n = 3*2^n + (-1)^(n+1).
Espero haberte ayudado.
-
Alex Domínguez
el 4/10/16Si A∈Mn×n(R) y b∈Mn×1(R) satisfacen que b≠0, Ab=0, entonces el sistema AX=0, donde X∈Mn×1(R) es la columna de incógnitas y 0 es la matriz columna nula de orden n×1: Seleccione una: a. Tiene como única solución X=0 b. No tiene solución c. Tiene infinitas soluciones ese es el ejercicio completo
Antonius Benedictus
el 4/10/16Como el sistema AX=0 es un sistema homogéneo, si es compatible determinado, cosa que sucede si det(A)≠0, solo tiene la solución trivial (el vector nulo). Como resulta que tiene una solución no trivial b≠0, el sistema es compatible e indeterminado. Por ello, tiene infinitas soluciones.
