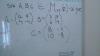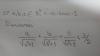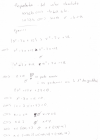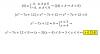Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Miguel
el 22/9/16

Hola amigos espero que me puedan ayudar, tengo examen de matrices he estado estudiando bastante y tengo una duda hacerla de este ejercicio que aparece en la imagen.
La pregunta es ¿para que valores de a y beta se satisfacen las siguientes igualdades?
a) (A +B) tendrían que estar los mismos números en los mismos lugares a=beta
B) A+B = c a=6 beta = -7

••0 voto/s
•
Matías Ignacio Loyola Galdames
el 23/9/16
No entendí la a)
aquí la b) Cualquier duda me dices

•0 voto/s
•

Cancelar
Keith Caballero Rodriguez
el 22/9/16

Me podrían ayudar con esta demostración

••0 voto/s
•
Antonius Benedictus
el 23/9/16
Keith, pon foto del enunciado original, por favor,

•0 voto/s
•

Cancelar
Juan
el 22/9/16

Necesito ayuda con este ejercicio de racionalización no entiende que sucede en el numerador del paso 2 al paso 3.

••0 voto/s
•
Axel Morales Piñón.
el 22/9/16
mejor ¿¿??

•1 voto/s
•

Cancelar
Sofía
el 22/9/16

No consigo avanzar más, cómo saco la inversa de la matriz?

••0 voto/s
•
Matías Ignacio Loyola Galdames
el 23/9/16
Cualquier duda me dices

•0 voto/s
•

Cancelar
Rocio
el 22/9/16

Pueden decirme si esta bien el ejercicio

••0 voto/s
•
Antonio Silvio Palmitano
el 22/9/16
Lo has resuelto correctamente.

•0 voto/s
•
Frank Rios
el 22/9/16
Los cálculos son correctos

•1 voto/s
•

Cancelar
razexx
el 22/9/16

He de encontrar los n° reales que verifican la siguiente condicion:

••0 voto/s
•
Antonius Benedictus
el 22/9/16
Va uno:

•1 voto/s
•
razexx
el 22/9/16
No acaba de enterder el proqie de lo de e^x>0

•0 voto/s
•
Antonius Benedictus
el 23/9/16
La función exponencial natural e^x es estrictamente positiva. Cualquier potencia de base positiva da siempre un número positivo, sea cual fuere el exponente.

•0 voto/s
•

Cancelar
razexx
el 22/9/16

En el siguiente ejercicio he de encontrar los n° reales que verifican la siguiente condicion: (no sé como continuar)

••1 voto/s
•
Alex Grattan
el 22/9/16

espero se vea bien y le entiendas, esas propiedades son importantes,saludos :)

•1 voto/s
•
Antonius Benedictus
el 22/9/16
Te explicamos, Razexx:

•1 voto/s
•
razexx
el 22/9/16
Lo que no entiendo es por qué se multiplica la ecuación por 2.
Muchas gracias amigo

•1 voto/s
•
Alex Grattan
el 22/9/16
perdon me eq uivoque no es la union sino la intersección te da un intervalo abierto de 3 a 4

•1 voto/s
•
razexx
el 22/9/16
¿Cual seria el conjunto entonces? (Dicho en palabras y en notación matematica) porque no entiendo los corchetes al revés de Antonio.
De verdad, perdón por las molestias, pero me juego la nota, y quiero entenderlo. De nuevo gracias

•0 voto/s
•
Alex Grattan
el 22/9/16
se multiplica por 2 porque pasas restando al otro lado de la desigualdad , y te queda una suma de 2 cosas iguales
mira tienes que ver el caso donde
x2 - 7x +12 < -x2 + 7x - 12
entonces
sumando x2 - 7x +12 de ambos lados te queda
2(x2 - 7x +12) < 0
multiplicas por 1/2
x2 - 7x +12 <0 t¿y empiezas a resolver

•1 voto/s
•
Alex Grattan
el 22/9/16
x esta en (3,4) intervalo abierto de 3 a 4

•1 voto/s
•
razexx
el 22/9/16
Ahora Alex si lo he entendido, muchas gracias pero sigo teniendo dudas en dos ejemplos. Los demás se hacerlos.

•0 voto/s
•

Cancelar
Rocio
el 22/9/16

Hola no se si estoy resolviendo bien me podrian ayudar

••0 voto/s
•
Frank Rios
el 22/9/16
no se que muy bien la foto Rocio

•0 voto/s
•
Frank Rios
el 22/9/16
Los cálculos son correctos igual si puedes me gustaria que subas una foto mas clara

•0 voto/s
•

Cancelar
Gaussiano
el 22/9/16

Hoola! Tengo una duda con el siguiente ejercicio, mi profesor de álgebra nos pidió que estudiáramos el rango de la matriz haciendo ceros en las filas. Bien, yo he logrado triangular la matriz (no sé si está bien), pero mi duda era si se podía reducir, si se podía hacer ceros a la derecha de los pivotes de cada fila. Gracias!

••0 voto/s
•
Antonio Silvio Palmitano
el 23/9/16
Para este tipo de ejercicio con elementos indeterminados expresados con la indeterminada t (theta), debes distinguir dos casos:
1) t = 0, sustituyes y queda una matriz con todos elementos numéricos que podrás reducir y escalonar fácilmente, y verás que su rango es 3;
2) t distinto de 0
Aquí es donde debes aplicar las operaciones elementales, y se arrastrarán expresiones con t a lo largo de la tarea:
|°) F3-->F3-F2 (obseva que los elementos de fila 3 quedan: < 0 , 0 , (t-1) >)
2°) F2-->3F2-tF1 (observa que los elementos de fila 2 quedan: < 0 , (9+t^2) , 3 >
Observa que el segundo elemento de fila 2 es distinto de cero por ser suma de términos positivos, por lo que planteamos:
3°) F1-->(9+t^2)F1+tF2 (si vas siguiendo todo con lápiz y papel, verás que queda trabajar solamente en la tercera columna)
Observa que los elementos de la tercera fila son: < 0 , 0 , t-1 >, por lo que distinguimos dos casos:
a) t = 1, que nos conduce a una tercera fila nula y el trabajo llegó a su fin porque ya tenemos que el rango es 2 como podrás ver fácilmente;
b) t distinto de 1, lo que nos permite continuar:
4°) F1-->(t-1)F1-3tF3 (observa que los elementos de la fila 1 quedan: < 3(9+t^2)(t-1) , 0 , 0 >
5°) F2-->(t-1)F2-3F3 (observa que los elementos de la fila 2 quedan: < 0 , (9+t^2)(t-1) , 0 >
Observa que a esta altura ya has obtenido una matriz diagonal, que en su diagonal principal tiene todos elementos distintos de cero, por lo que su rango es 3:
Espero haberte ayudado.

b) t distinto de 1, lo que nos permite continuar:
;

•0 voto/s
•
Gaussiano
el 23/9/16
Gracias Antonio

•0 voto/s
•

Cancelar
José Manuel
el 22/9/16

Ayuda con este:

••0 voto/s
•
César
el 22/9/16
Va Jose Manuel,
en la foto salio cortada la ultima linea
l(t)=0 => -0.5t+3=0 t=6 minutos

•1 voto/s
•

Cancelar