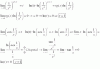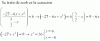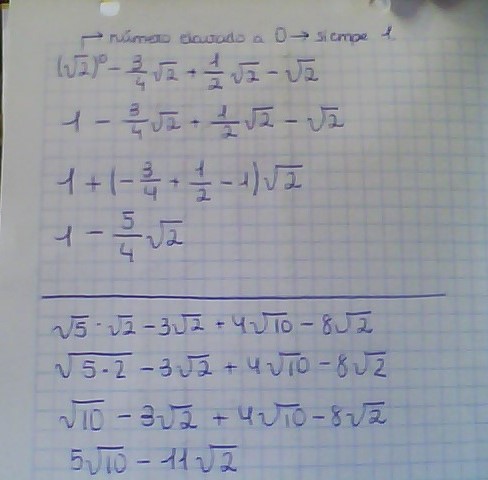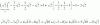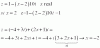Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Luìs Lòpez
el 22/9/16
^{Hola, me podrían ayudar con el siguiente ejercicio:}
^{¿qué valor del parámetro "a" estos vectores forman un sistema generador del espacio vectorial R3?}
^{V1= (-2,3,2), V2=(a+2,0,3) V3=(5,3,a)}
^{Me confunde el vector 2. Intento calcular el rango y ver si son Lineal mente independiente pero no consigo obtener el valor de a.}
^{el resultado es:}
- ^{"a" es igual o diferente de 5}
- ^{"a" es igual o diferente de -5}
••0 voto/s
•
Antonio Silvio Palmitano
el 22/9/16
Puedes plantear un determinante, cuyas filas son las componentes de cada vector, igualar a cero.
Cuando desarrolles el determinante te quedará un polinomio y, al estar igualado a cero, una ecuación con incógnita a.
Luego la resuelves, y los valores de a que son solución son los valores para los cuáles los vectores no son linealmente independientes. Por ello, concluirás que si a es distinto de a1 y de a2 (a1 y a2 son las soluciones de la ecuación), el conjunto de vectores es una base de R^3.
Haz el intento, y aquí estaremos para ayudarte si surge algún inconveniente.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Rocio
el 22/9/16

Hola me podrian ayudar con ejercicio de números complejos necesito, un solo apartado los otros los quiero hacer yo

••0 voto/s
•
César
el 22/9/16
Rocio impertativo leerse la teoria cielo.
si sigues con dudas , nos cuentas

Números complejos
•1 voto/s
•

Cancelar
Alba
el 22/9/16

Hola, necesito ayuda con estos dos ejercicios de límites. Gracias de antemano.

••0 voto/s
•
César
el 22/9/16
Alba usa derivacion logaritmica

•0 voto/s
•
Antonius Benedictus
el 22/9/16
Te va el primero, Alba:

•0 voto/s
•

Cancelar
Wayner
el 22/9/16

Buenas amigos, me podrian ayudar.en este ejeecicio de ecuacion logaritmicas, me quede estancado y no se que mas hacer. La respuesta del ejercicio es la opcion a) -6

••0 voto/s
•
César
el 22/9/16

•0 voto/s
•

Cancelar
Mario
el 22/9/16

Holaa necesito ayuda con este ejercicio,concretamente con el 122 apartado a y c. Para el a es si se puede introducir la a en el radical a pesar de que este tenga una resta en su numerador, y en cuanto al c, es si se puede meter un numero negativo en un radical. Gracias por adelantado.

••0 voto/s
•
César
el 22/9/16
Te van varios , intenta seguir tu

•0 voto/s
•

Cancelar
Pablo
el 22/9/16

Alguien inteligente...
Gracias de antemano. Saludos.

••0 voto/s
•
Iria Seijo Porto
el 22/9/16

Yo lo haría así
•0 voto/s
•
César
el 22/9/16
Yo pero solo un poco

•0 voto/s
•
Pablo
el 22/9/16
César, ¿puedes decirme la teoría o cómo lo resolviste? He visto los vídeos, pero estos ejercicios son más complejos. Gracias .

•0 voto/s
•
Pablo
el 22/9/16
En concreto, en el primer ejercicio no entiendo la raíz de 2 y el paréntesis que le sigue.

•0 voto/s
•
César
el 22/9/16
tienes que sacar factor comun
Factor comun Factor comun

Factor comun
•0 voto/s
•
Pablo
el 22/9/16
Veo el vídeo y te comento. Gracias . Saludos.

•0 voto/s
•

Cancelar
Judith
el 22/9/16

¡Buenas! Este año he empezado bachiller, y me he atascado con las operaciones relacionadas con el valor absoluto, he estado viendo los vídeos pero en la mayoría están igualados o con inecuaciones. Me podríais asegurar q he hecho bn el ejercicio, aunque no lo se terminar ya que no se si poner 0 o -2. Muchisimas gracias!

••0 voto/s
•
Antonio Silvio Palmitano
el 22/9/16
Has planteado bien los valores absolutos como funciones a trozos, y sus puntos de corte:
|x| corta en 0, y |x+2| corta en -2,
luego, como las dos funciones valor absoluto tienen dominio R, observa que los puntos de corte nos determinan tres intervalos:
a) (-inf,-2), para él: |x| = -x y |x+2| = -(x+2), y la expresión queda: x -x - (x+2) = - (x+2) = - x - 2
-2, para este punto: |-2| = 2 y |-2+2| = 0, y la expresión queda: -2 + 2 + 0 = 0
b) (-2,0), para él: |x| = -x y |x+2| = x + 2, y la expresión queda: x - x + x + 2 = x + 2
0, para este punto: |0| = 0 y |0+2| = 2, y la expresión queda: 0 + 0 + 2 = 2
c) (0,+inf), para él: |x| = x y |x+2| = x + 2, y la expresión queda: x + x + x + 2 = 3x + 2.
Esta es una manera de evaluar intervalos de validez de una expresión con sumas o restas de valores absolutos: determinar los puntos de corte para cada trozo, luego establecer los intervalos y luego evaluar la expresión según los trozos válidos para cada intervalo, y también hay que evaluar la expresión en los puntos de corte.
Espero haberte ayudado.

•1 voto/s
•
César
el 22/9/16
Va judith

•1 voto/s
•
Judith
el 22/9/16
Antonio Silvio Palmitano, agradezco tu respuesta pero no me termino de aclarar. No se si me has corregido o es otra opción posible, de todas formas ya te digo muchisimas gracias, la próxima mas y mejor, jj.
En cuanto a César, lo he entendido bastante bien, lo único que me vienen un par de dudas:

•0 voto/s
•

Cancelar
Iria Seijo Porto
el 22/9/16

Hola. Empiezo 1º bach. Estuvimos repasando el error absoluto y relativo. Pero tengo un problema cuando me piden que ajuste ese error a una determinada cifra. P.ej. -- como garantizar que:
a. el error absoluto sea menor que 10 elevado a menos 6
b. el error relativo sea inferior a 10 elevado a menos 4
También necesito entender esto que puso en el encerado
Ayudaaa por favor graciaaas

••0 voto/s
•
David
el 26/9/16
Si Ea= 1235,2718 - Valortomado <10^(-6), simplemente despeja... 1235,2718-10^(-6) <Valor tomado
Cualquier valor que tomes que cunmpla esa inecuacion te garantiza un error absoluto inferior a 10^(-6)...

Y para el Error relativo, lo mismo... Debe cumplirse que (1235,2718 - Valortomado) / 1235,2718 <10^-(4)... Resuelve la inecuación...

•1 voto/s
•

Cancelar
Jordi Ramos
el 22/9/16

Hola amigos estoy empezando estudiar números complejos y no entiendo este ejercicio me podrían ayudar.

••0 voto/s
•
Antonio Silvio Palmitano
el 22/9/16
1) z = 1- (x-2)*10i
distribuimos en el segundo término de la derecha:
z = 1 - x*10i + 20i
agrupamos términos imaginarios y queda:
z = 1 + ( -10x + 20)i
Observa que para que z sea real, debe cumplirse:
-10x + 20 = 0, despejamos y queda: x = 2.
2) z = (- 4 + 3i) + (2x + 1)i
distribuimos agrupamientos y queda:
z = - 4 + 3i + 2xi + i
reducimos términos sejantes:
z = - 4 + 2xi + 4i
agrupamos términos imaginarios:
z = - 4 + (2x + 4)i
observa que para que z sea real debe cumplirse: 2x + 4 = 0, despejamos y queda: x = - 2.
Espero haberte ayudado.

•0 voto/s
•
César
el 22/9/16
Va jordi mirate la teoria un poco

Números complejos
•0 voto/s
•
Antonius Benedictus
el 22/9/16
Como lo tengo hecho, también te lo mando:

•0 voto/s
•

Cancelar
Antonio Marin
el 22/9/16

En el método de Gauss para conseguir la inversa de una matriz, el orden en el que se opera con las filas es siempre el mismo o podemos sumar/restar... según nos interese sin seguir un orden especifico?

••0 voto/s
•
Antonius Benedictus
el 22/9/16
Puedes utilizar cualquier transformación elemental, pero sólo con las filas y con TODA la fila en cada caso.

•1 voto/s
•

Cancelar