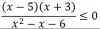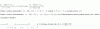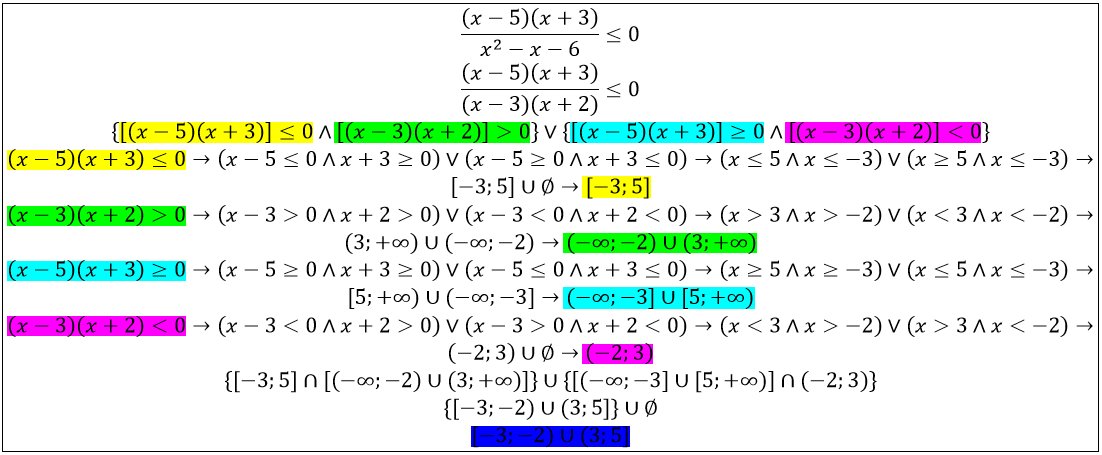A ver si te sirve:

Debbie...

Primero saca las raíces del numerador y luego las del denominador. Después, representas esos valores en una recta como la de la foto. 

Las raíces del denominador no tienen sentido, pero si la tienen las del numerador.

El intervalo que verifica tu ecuación es [-3 ; -2) U (3 ; 5]. el -3 y el 5 se incluyen porque tu inecuación dice menor igual a 0, y si reemplazas -3 y 5 en la ecuación da como resultado 0. Eso también sucede para -2 y 3 peor no se tienen en cuenta porque son raíces del denominador.

Por último, buscas valores entre las raíces y reemplazas en la fórmula. Se tiene que cumplir que sea menor igual, osea, resultado negativo e igual a 0.

Si tenés dudas, pregunta.

Acá hay un video de ejercicios de inecuaciones con rectas: https://www.youtube.com/watch?v=6cVczQWNtqk 

Ahí va la foto...

Va Debbie 

Debbie esta bien copiado el ejercicio? así es muy complicado para hacerlo paso a paso; en cuanto lo tenga lo envío

Puedes comenzar por factorizar el denominador por medio de la fórmula resolvente para ecuaciones polinómicas cuadráticas, y verás que puede ser escrito: (x+2)(x-3), luego la desigualdad queda:

(x-5)(x+3) / (x+2)(x-3) <= 0.

Luego, observa que tenemos dos opciones en primera instancia:

1) (x+2)(x-3) > 0, luego pasamos multiplicando en la desigualdad (observa que el denominador es positivo) y queda: (x-5)(x+3) <= 0.

2) (x+2)(x-3) < 0, luego pasamos multiplicando en la desigualdad (observa que el denominador es negativo) y queda: (x-5)(x+3) >= 0.

Luego vamos a cada una de las opciones (observa que a su vez tenemos dos nuevas opciones en cada caso:

1a) x+2>0, x-3>0 y (x-5)(x+3) <= 0.

1b) x+2<0, x-3<0 y (x-5)(x+3) <= 0.

2a) x+2>0, x-3<0 y (x-5)(x+3) >= 0.

2b) x+2<0, x-3>0 y (x-5)(x+3) >= 0.

Luego, observa que en cada una de estas cuatro opciones se tienen otras dos (observa que en cada opción los elementos x cumplen cuatro condiciones), por lo tanto tenemos:

1a1) x+2>0, x-3>0, x-5>=0 y x+3<=0, a lo que corresponde: x>-2, x>3, x>=5 y x<=-3, lo que nos lleva al intervalo vacío.

1a2)x+2>0, x-3>0 y x-5<=0 y x+3>=0, a lo que corresponde: x>-2, x>3, x<=5 y x>=-3, lo que nos lleva al intervalo (3,5].

1b1) x+2<0, x-3<0 y x-5>=0 y x+3<=0, a lo que corresponde: x<-2, x<3, x>=5 y x<=-3, lo que nos lleva al intervalo vacío.

1b2) x+2<0, x-3<0 y x-5<=0 y x+3>=0, a lo que corresponde: x<-2, x<3, x<=5 y x>=-3, lo que nos lleva al intervalo [-3,-2).

2a1) x+2>0, x-3<0 y x-5>=0 y x+3>=0, a lo que corresponde: x>-2, x<3, x>=5 y x>=-3, lo que nos lleva al intervalo vacío.

2a2) x+2>0, x-3<0 y x-5<=0 y x+3<=0, a lo que corresponde: x>-2, x<3, x<=5 y x<=-3, lo que nos lleva al intervalo vacío.

2b1) x+2<0, x-3>0 y x-5>=0 y x+3>=0, a lo que corresponde: x<-2, x>3, x>=5 y x>=-3, lo que nos lleva al intervalo vacío.

2b2) x+2<0, x-3>0 y x-5<=0 y x+3<=0, a lo que corresponde: x<-2, x>3, x<=5 y x<=-3, lo que nos lleva al intervalo vacío.

Por lo tanto, el conjunto solución, con notación de intervalo queda: 

[-3,-2) u (3,5].

Espero haberte ayudado.

Puedes hacer el mismo planteo del Teorema del Valor Medio para la función g, tal como lo hemos hecho para la función f, y quedan:

f ' (c) = ( ( f(b) - f(a) ) / (b - a) )

g ' (c) = ( ( g(b) - g(a) ) / (b - a) )

Luego, como sabemos que g ' (c) es distinto de 0, podemos hacer el cociente miembro a miembro, simplificamos en el segundo miembro y queda:

f ' (c) / g ' (c) = ( ( f(b) - f(a) ) / (b - a) ) / ( ( g(b) - g(a) ) / (b - a) ).

Este es el Teorema de Cauchy, y lo hemos demostrado apelando al Teorema de Lagrange, que es un teorema anterior.

Espero haberte ayudado.

Antes me dijistes que g ' (c) es igual a cero. Ahora por que g '(c) es distinto de cero ? Muchas gracias me ha servido de gran ayuda

Observa bien, Alejandro. En el ejercicio anterior teníamos OTRA función a la que llamamos, por desgracia, g.

Ésta tenía la siguiente expresión:

g(x) = f(x) - ( (f(b) - f(a)) / (b-a) )(x - a)

que es la que usamos para demostrar el Teorema de Lagrange.

En este ejercicio, en el que debemos demostrar el Teorema de Cauchy, trabajamos con dos funciones:

f y g, que cumplen con las hipótesis del Teorema de Lagrange, por lo que para ambas planteamos:

f ' (c) = ( ( f(b) - f(a) ) / (b - a) )

g ' (c) = ( ( g(b) - g(a) ) / (b - a) ).

La confusión viene de allí, si prefieres, a la función que construimos para demostrar el Teorema de Lagrange anteriormente le podemos dar otro nombre, por ejemplo h(x).

Espero haber aclarado tu duda.

Steffani: Haz un diagrama de árbol, donde vas poniendo las probabilidades, e identifica las situaciones con lo que te enviamos:

Te sugiero veas los vídeos de probabilidad...

Alejandro...

Teorema de valor medio (Lagrange)

Hace poco dí un parcial de Análisis y justo me acordé del apunte.

Ahí va la foto. . . 

Construimos la función cuya expresión es:

g(x) = f(x) - ( ( f(b) - f(a) ) / (b - a) )(x - a)

Observa que la función g es continua y derivable, por ser resta entre funciones continuas y derivables.

Observa que g(a) = f(a) y que g(b) = f(a).

Por lo tanto se cumplen las hipótesis del Teorema de Rolle y podemos asegurar que existe c perteneciente al intervalo (a,b) tal que g ' (c) = 0 (*).

Derivamos la función g y su expresión queda:

g ' (x) = f ' (x) - ( ( f(b) - f(a) ) / (b - a) ).

Evaluamos para el valor c, aplicamos la igualdad señalada (*) y tenemos que:

f ' (c) - ( ( f(b) - f(a) ) / (b - a) ) = 0, hacemos pasaje de término y llegamos finalmente a:

f ' (c) = ( ( f(b) - f(a) ) / (b - a) ).

Este es el Teorema del Valor Medio de Lagrange, y lo hemos demostrado apelando al Teorema de Rolle, que es un teorema anterior que has visto en clase.

Espero haberte ayudado.

:D Gracias a tí! Un abrazo!!! #nosvemosenclase

Llamemos x a la longitud de la base de uno de los rectángulos, y llamemos y a la longitud de la altura de uno de los rectángulos.

Por lo tanto, el área total queda expresada: At = 6xy.

Luego, observa a partir de la figura que con los 30 metros de alambre se deben cubrir 12 bases de rectángulos (las seis inferiores y las seis superiores) y 7 alturas de rectángulos, por lo tanto planteamos:

6x + 7y = 30, de aquí despejamos una de ellas, por ejemplo: y = 30/7 - (6/7)x,

luego sustituimos en la expresión del área total, y queda:

At(x) = 6x( 30/7 - (6/7)x ).

Para establecer el dominio de la función, debemos tener en cuenta que el área es una magnitud positiva y, como su expresión es un producto de dos factores, éstos deben ser ambos positivos y, además, recordemos que x es una longitud, por lo que debe ser estrictamente positiva. Por lo tanto planteamos:

6x > 0, dividimos en ambos miembros por 6 y queda: x > 0;

30/7 - (6/7)x > 0, hacemos pasaje de término y queda:

- (6/7)x > -30/7, hacemos pasaje de factor negativo (recordemos que se invierte el sentido de la desigualdad, resolvemos y queda:

x < 5.

Por lo tanto, el dominio de la función área total es (en notación de intervalo): D = (0,5).

Espero haberte ayudado.

Muchas Gracias por la ayuda!

El problema es que me dan números altísimos  a la hora de hacer el sistema y no me sale

yo he tomado los últimos dígitos de cada año y lo he resuelto, observa 

para que lo veas. solo te faltaría reemplazar 1 y 3 en la ecuación para obtener los valores de esos años, suerte ;-)

Pero cómo es que coges el último dígito? Entiendo que es más práctico pero, es lo mismo?? Yo he cogido el número entero

es lo mismo; hasta creo que podrías escoger otros valores equivalentes, por ejemplo: 1990=2 ->1991=4->1992=6... y te saldría otro ecuación equivalente ;-)

Ramiro...

Cotgx= cosx / senx

Con esa info saca tu conclusión y luego dime. Éxitos

Observa que a partir de la sugerencia del Colega Lucas, puedes elevar al cuadrado y la identidad queda:

(cotgx)^2 = (cosx)^2 / (senx)^2

luego, a partir de la identidad fundamental (o pitagórica) tienes:

(cosx)^2 + (senx)^2 = 1.

Por lo que todo se reduce a resolver el sistema de ecuaciones (reemplazamos el valor de la cotangente de x, que es dato de tu enunciado, y resolvemos su cuadrado):

(cosx)^2 / (senx)^2 = 9/16

(cosx)^2 + (senx)^2 = 1.

Observa que se trata de un sistema de dos ecuaciones con dos incógnitas que, al ser despejadas, conducirán a dos soluciones, ya que hay un ángulo del primer cuadrante que tiene cotangente +3/4, cuyo seno y su coseno son positivos, y hay otro ángulo en el tercer cuadrante, que también tiene cotangente +3/4, pero su seno y su coseno son ambos negativos.

Espero haberte ayudado.

así Pou ;-)