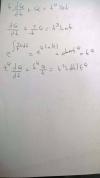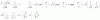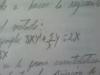-


Juan
el 4/9/16Pues ahora mismo no puedo decirte datos exactos porque no tengo mucho tiempo, pero el procedimiento parece ser:
1. Hallar el área de la figura, todo ello en relación a una sola variable (al ser las piezas externas iguales dos a dos, es suficiente con hallar el área de una mitad, que es un triángulo, y duplicarla)
2. Con ese área, hacer una función y estudiar sus máximos y mínimos (Con la primera derivada y sus intervalos de crecimiento/decrecimiento debería ser sencillo)
3. Tras hallar el máximo, usar esa variable para encontrar, con trigonometría, las longitudes de las diagonales
Espero haberte ayudado, me gustaría darte números, pero voy con poco tiempo.
P.D: Acabo de darme cuenta que al no tener ningún dato exacto de área, seguramente la función tienda a infinito en algún caso. Para evitarlo, intenta relacionar las longitudes de las dos diagonales para que eso te de tu variable, y así el resultado será que una barra será x, y la otra un cierto número mayor que x (kX)
-
Buenas tardes,
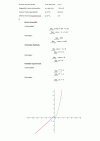
Adjunto la resolución que realicé del ejercicio de la montaña rusa, están las expresiones analíticas de las funciones, una gráfica y los estudios de continuidad y derivabilidad. ¿Son correctos?
Muchas gracias!!!!!!!!.
Raisa
- hace 2 días, 23 horas
Buenas tardes,
Se me plantea el siguiente ejercicio: "Diseñar un tramo de 100 metrs de una montaña rusa que contenga tramos con formas gráficas: exponencial, recta, parabólica y sinusoidal". Debo plantear un bosquejo gráfico y también las expresiones analíticas. Yo diseñé un tramo en el siguiente orden: parábola, sinusoidal, exponencial y recta. Mi duda es la siguiente, la función total, o sea la suma de éstas funciones. debe ser continua, ya que los carros no deben despegarse de los rieles. ¿Cómo aseguro ésta condición?
Gracias!comment
0 voto/s
David
- hace 2 días, 5 horas
Para asegurar que es continua, en los puntos de "transición" de tu funcion a trozos, la funcion por la izquierda y la funcion por la derecha deben tender al mismo numero...
Debes por tanto conseguir que las funciones tomen el mismo valor de "y" para esos valores de "x" que hayas elegido. si quieres puedes enviarnos una foto con todo lo conseguido y te orientamos para que puedas rematar el ejercicio. -
Hola, Amigos de Unicoos: necesito ayuda con este ejercicio, Determine las coordenadas de las proyecciones ortogonales del vector Q= (-3,2,1) sobre los ejes y planos coordenados.


Antonio Silvio Palmitano
el 4/9/16De acuerdo con el Colega Gabriel.
Observa que la proyección sobre el plano coordenado XY tiene tercera componente nula (la que corresponde al eje OZ), que la proyección sobre el plano coordenado XZ tiene segunda componente nula (la que corresponde al eje OY), y que la proyección sobre el plano coordenado YZ tiene primera componente nula (la que corresponde al eje OX). Observa que en los tres casos, las demás componentes del vector Q se mantienen invariantes.
Espero haberte ayudado.
-

Gabriel
el 4/9/16A ver, el problema no es que esté muy bien planteado puesto que el ángulo que dicen ser de 30º es un ángulo obtuso, pero bueno...
El ángulo ξ, al ser opuesto por el vértice, también es 30.
δ y k, son también ángulos opuestos por el vértice, por lo que son iguales. Su valor... δ=k=(360-2ξ)/2=150
Y por semejanza β=30, γ=α=150
Los vértices no se pueden calcular puesto que no nos dan distancias ni medidas de otros ángulos para poder calcularlos.
Saludos.
-


Antonio Silvio Palmitano
el 4/9/16Observa que estás tratando con una ecuación diferencial lineal, de primer orden y primer grado, te recomiendo revises tus apuntes de clase, y mires los vídeos.
En tu trabajo, has hecho bien las cosas hasta la segunda línea, en que la ecuación queda:
dQ/dt + (1/t)Q = t^3 * lnt
Hacemos la integral auxiliar:
A = Integral (1/t)dt = lnt (en este paso no introducimos la constante de integración), luego planteamos la integral:
Luego pasamos a la solución general:
Q(t) = e^(-lnt) * ( Integral ( e^lnt * t^3 * lnt )dt + C ), a continuación resolvemos las composiciones entre exponenciales y logaritmos y queda:
Q(t) = (1/t) * ( Integral ( t * t^3 * lnt + C ), operamos en la expresión que quedó para integrar y queda:
Q(t) = (1/t) * ( Integral ( t^4 * lnt + C).
Desde aquí puedes continuar, y observa que la integral que queda por resolver la puedes abordar con el método de las partes, como seguramente has visto en clase, lo haces y verás que la solución general es:
Q(t) = (1/t) * ( (1/5) * t^5 * lnt - (1/25) * t^5 + C ) = (1/5) * t^4 * lnt - (1/25) * t^4+ C/t.
Recordemos la forma general de este tipo de ecuaciones:
dy/dt + Py = R, donde P y R son funciones de t.
Para resolverla, planteamos la integral auxiliar:
A = Integral (Pdt) (observa que nos queda A, que es una nueva función de t, y que no agregamos la constante de integración).
Luego vamos a la solución general:
y = e^(- A) * Integral ( e^A * R * dt + C ), donde ahora si C es la constante de integración de la solución general.
Espero haberte ayudado.
-
-
Podrían ayudarme?
1. Una gran empresa consulta a sus empleados sobre un plan de primas. El plan apoyado por el 65% de todos los trabajadores del turno de noche y por el 40% de las mujeres trabajadoras. Además, el 50% de los empleados pertenecen al turno de noche y el 30% de todos los empleados son mujeres. Finalmente, el 20% de los trabajadores del turno de noche son mujeres.
a) ¿Cuál es la probabilidad de que un empleado elegido al azar sea una mujer que apoya el plan?
b) ¿Cuál es la probabilidad de que un empleado elegido al azar sea una mujer y/o un trabajador del turno de noche?
c) ¿Es el sexo del empleado independiente de si trabaja o no en el turno de noche?
d) ¿Cuál es la probabilidad de que una empleada pertenezca al turno de noche?
e) Si el 50% de los empleados varones apoyaron el plan. ¿Cuál es la probabilidad de que un empleado elegido al azar no trabaje durante el turno de noche y no apoye el plan?