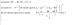Puedes comenzar por designar incógnitas:
L = tiempo total empleado por Leia;
C = tiempo total empleado por Chewbacca,
x = tiempo empleado por Chewbacca en realizar los primeros 14 movimientos.
Luego vamos al enunciado, y buscamos relaciones entre las incógnitas:
"El tiempo que emplea Leia en los primeros 14 movimientos es triple que el empleado por Chewbacca, mientras que en los restantes movimientos ambos emplearon 35 minutos" De aquí tenemos:
C = x + 35
L = 3x + 35
"Sabiendo que el tiempo utilizado por Chewbacca en el total de la partida es 3/4 partes del utilizado por Leia". De aquí tenemos:
C = (3/4)L.
Luego sustituyes las expresiones de C y L de las primeras dos ecuaciones, en la tercera y queda:
x + 35 = (3/4)(3x + 35)
distribuyes a la derecha y queda:
x + 35 = (9/4)x + 105/4
realizas pasajes de términos y queda:
x - (9/4)x = 105/4 - 35
reduces términos semejantes en ambos miembros y queda:
(-5/4)x = -35/4
haces pasaje de factor como divisor y queda:
x = (-35/4) / (-5/4)
resuelves y llegas a:
x = 7 minutos.
Luego reemplazas en las expresiones de C y L y llegas a:
C= 7 + 35 = 42
por lo que tenemos:
C = 42 minutos;
L = 3*7 + 35 = 21 + 35 = 56
por lo que tenemos:
L = 56 minutos.
Espero haberte ayudado.
L =

49)
Partimos de la ecuación: x = y^2 - 5, hacemos pasaje de término y queda:
x + 5 = y^2, hacemos pasaje de potencia como raíz y queda:
V(x + 5) = y, que nos conduce a dos funciones, cuyas expresiones son:
f1 (x) = +V(x + 5)
f2(x) = -V(x + 5)
Para las dos, la condición que debe cumplir el argumento de la raíz cuadrada es:
x + 5 >= 0, hacemos pasaje de término y queda:
x >= -5,
por lo que el dominio puede expresarse para ambas funciones:
D = {x perteneciente a R: x >= 5]
o como intervalo:
D = [5 , +inf).
50)
Partimos de la ecuación: x^2 - 4y^2 = 16, hacemos pasajes de términos y queda:
x^2 - 16 = 4y^2, dividimos por 4 en todos los términos y queda:
x^2 / 4 - 4 = y^2, hacemos pasaje de potencia como raíz y queda:
V(x^2 / 4 - 4) = y, que nos conduce a dos funciones, cuyas expresiones son:
f1 (x) = +V(x^2 / 4 - 4)
f2(x) = -V(x^2 / 4 - 4)
Para las dos, la condición que debe cumplir el argumento de la raíz cuadrada es:
x^2 / 4 - 4 >= 0, hacemos pasaje de término y queda:
x^2 / 4 >= 4, hacemos pasaje de divisor como factor, resolvemos a la derecha y queda:
x^2 >= 16
luego hacemos pasaje de potencia (cuadrado) como raíz (cuadrada), recordando que: x^2 = |x|^2 y queda:
|x| >= |V(16)|, resolvemos a la derecha y queda:
|x| >= 4, que nos conduce a dos opciones:
x <= -4 o x >= 4
por lo que el dominio puede expresarse para ambas funciones:
D = {x perteneciente a R: x <= -4 o x >= 4}
o como unión de intervalos:
D = (-inf , -4] u [4 , +inf).
Espero haberte ayudado.

Debes recordar que el producto de matrices no es conmutativo, por lo tanto AB es distinto de BA (salvo excepciones).
Como estamos trabajando en general con matrices cuadradas con elementos reales con n filas y n columnas, planteamos:
(A + B)(A + B) = distribuimos (recuerda que debemos mantener el orden de los factores, ya que el producto no es conmutativo entre matrices) y queda:
= AA + AB + BA + BB que es distinto de AA + 2AB + BB, porque no podemos afirmar que AB es igual a BA para luego sumar los dos términos centrales.
Por lo tanto, la afirmación es falsa.
Espero haberte ayudado.

Observa que si la matriz C es invertible y su matriz inversa es C^(-1) tenemos:
AC = BC, luego multiplicamos por derecha por la matriz inversa de C y queda:
(AC) * C^(-1) = (BC) * C^(-1), luego como el producto de matrices es asociativo podemos escribir:
A * (C * C^(-1)) = B * (C * C^(-1)), luego recordando que el producto de la matriz C por su matriz inversa es igual a la matriz identidad de orden n, tenemos:
A * I = B * I, luego por propiedad del producto de una matriz por la matriz identidad llegamos a:
A = B.
Por lo tanto, concluimos que si la matriz C es invertible, entonces la proposición es verdadera, y si existen matrices que cumplen con ella.
Espero haberte ayudado.

Va la ayuda, Freitas:

Va, punk.

Hola, punk:

http://www.gyplan.com/es/eqcubic_es.html

a ver si te vale así

Podrias mandar de nuevo se ve muy desenfocada