logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    Facundo Meier
    el 28/7/16

    Profes, nuevamente necesito ayuda por favor con la siguiente función, |x^2-1|
    Al analizar la inyectividad de la grafica , me doi cuenta que la función no es inyectiva, pero cuando lo hago analiticamente , veo que si lo es
    Analiticamente:
    |x1^2-1| = |x2^2-1|
    x1^2-1 x2^2-1 entonces x 1 es igual a x2
    Muchas gracias

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/7/16

    Debes tener en cuenta que la igualdad con valores absolutos siempre implica dos opciones:
    |u| = |v|, de la cuál se desprenden:
    a) u = v, con u >= 0 y v >= 0, o también u < 0 y v < 0
    b) u = -v, con u >= 0 y v < 0, o también u < 0 y v >= 0.
    Observa que has intentado plantear la opción a), que has iniciado en forma correcta:
    |x1^2 - 1| = |x2^2 - 1|
    Luego, siguiendo la opción a) que corresponde a que los dos argumentos tengan igual signo:
    x1^2 - 1 = x2^2 - 1
    Luego, por propiedad cancelativa (que has aplicado en forma correcta):
    x1^2 = x2^2
    Aquí debes tener en cuenta cómo se simplifica una raíz cuadrada con una potencia de exponente dos: V(x^2) = |x|, en nuestro caso, tomando raíz cuadrada en ambos miembros:
    V(x1^2) = V(x2^2)
    |x1| = |x2|
    Y esta igualdad nos conduce a dos opciones:
    x1 = x2 (que es la opción que has encontrado), o también:
    x1 = -x2.
    Ya puedes ver que la función no es inyectiva.
    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    victor
    el 28/7/16
    flag

    Buenas tardes unicoos!!
    Me pasarían las siguientes tablas?....
    Distribución de Probabilidad Binomial Acumulada
    Distribución de Probabilidad de Poisson Acumulada

    Desde ya, muchísimas gracias!!

    reply•thumb_up•0 voto/s•flag
    icon

    David
    el 1/8/16

    Si buscas en google esas dos tablas, en imagenes, encontrarás decenas de ellas...

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Axel Morales Piñón.
    el 28/7/16

    Una manita con esto;

    reply•thumb_up•0 voto/s•flag
    icon

    Sebastian Quintero
    el 28/7/16

    tienes que hacer el cambio u=y/x y sale una homogenea por variables separables

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    nada
    icon

    Antonius Benedictus
    el 28/7/16

    Es así, amigo Peter:

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Toby
    el 28/7/16

    Hola unicoos, ayudenme hallando el área bajo la curva y²-4x=0 entre la recta x=-1 y x=0 y el eje de las abscisas.
    Gracias de antemano..

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/7/16

    Por favor, verifica el enunciado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Toby
    el 28/7/16

    Es un mas no menos, disculpe.
    y²+4x=0

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Luis Cano
    el 29/7/16

    Despejamos "y" de la ecuacion de la parábola: y²+4x=0 → y²=-4x→y=±√(-4x)
    Como nos interesa la parte superior de la parábola tomamos: y=√(-4x)
    Ahora solo debemos resolver una integral sencilla que te dejo en la imagen :)

    Como nos interesa la parte superior de la parábola tomamos: y=√(-4x)
    Ahora solo debemos resolver una integral sencilla que te dejo en la imagen :)">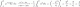

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Enrique
    el 28/7/16

    En el ejercicio 48 , me pide sacar el angulo que forma con la direccion positiva de las x , he sacado la ecuación de la mediatriz que pedía(no se si habré acertado a sacarla bien ), ¿¿alguna pista?? No encuentro fórmulas para sacarlo.

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 28/7/16

    Te explicamos, Enrique:

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Antonio Silvio Palmitano
    el 28/7/16

    Observa que el puno medio entre los puntos dados es D(2,-1), cuyas coordenadas son los promedios de las coordenadas correspondientes de los puntos dados.
    Luego, puedes calcular la pendiente de la recta que contiene al segmento determinado por los puntos dados:
    m = (-2 - 0)/(1 - 3) =-2 / (-2) = +1
    Luego, como la recta mediatriz es perpendicular a la recta que contiene a los puntos dados, calculamos su pendiente por medio de la relación de perpendicularidad.
    M = -1/m = -1/(+1) = -1
    Luego, como la recta mediatriz contiene al punto medio del segmento (punto D(2,-1) y su pendiente es -1, planteamos su ecuación
    y - (-1) = -1(x - 2)
    luego distribuimos, hacemos pasaje de término y reducimos términos semejante y llegamos a la ecuación cartesiana explícita de la recta mediatriz:
    y = -1x +1.
    Por último, recuerda que se llama pendiente de una recta a la tangente trigonométrica del ángulo que forma dicha recta con el semieje positivo de abscisas, por lo que tenemos para la recta mediatriz:
    tan(a) = M
    tan(a) = -1
    componemos con la función inversa de la tangente y tenemos:
    a = arctan(-1)
    a = 3pi/4 (o 135°).
    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Malen Zuñiga
    el 28/7/16

    Hola únicos , necesitaría que me explicaran como poder resolver estos problemas , que no se lo que tengo que hacer . Ejercicio 1 ) a y b

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/7/16

    a)
    Podemos expresar las capacidades de los dos recipientes:
    Capacidad del vaso = (1/5)litro
    Capacidad de la jarra = (2 y 1/2)itros = (2 + 1/2)litros = (5/2)litros.
    Luego presta atención a la pregunta: "¿Cuántos vasos se pueden llenar con el contenido de una jarra?
    Para tratar de responder, llamemos x a la cantidad de vasos a llenar, y planteemos una regla de tres simple (proporcionalidad):
    (1/5)litro corresponde a 1 vaso
    (5/2)litros corresponderán a x vasos
    Luego tenemos la proporción:
    (1/5) / (5/2) = 1 / x
    luego hacemos pasajes de divisores como factores y queda:
    (1/5)x = 1(5/2)
    Resolvemos a la derecha de la igualdad y queda:
    (1/5)x = 5/2
    Luego hacemos pasaje de factor como divisor y tenemos:
    x = (5/2) / (1/5)
    Resolvemos y queda:
    x = 25/2
    Luego, podemos escribir:
    x = (24 + 1)/2
    Luego distribuimos el denominador y queda:
    x = 24/2 + 1/2
    Simplificamos en el primer término de la derecha y tenemos:
    x = 12 + 1/2.
    Ahora podemos responder:
    Con el contenido de una jarra se pueden llenar doce vasos y medio.

    b)
    Puedes llamar x a la suma de dinero que había al comienzo en la alcancía, y debes tener en cuenta que cada uno de los chicos retiró (1/2)x.
    Luego, presta atención a las consignas del enunciado:
    "Ignacio gastó 1/3 de lo que tenía", lo que escribimos: Gasto de Ignacio = (1/3)(1/2)x = (1/6)x,
    "Ana gastó 7/9 de su mitad", lo que escribimos: Gastos de Ana = (7/9)(1/2)x = (7/18)x.
    Ahora podemos sumar para obtener el gasto total: Gasto total = (1/6)x + (7/18)x = (1/6 + 7/18)x = (10/18)x = (5/9)x.
    Luego podemos responder:
    El gasto entre los dos resultó ser cinco novenos de la cantidad total de dinero contenido inicialmente en la alcancía.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Miguel
    el 28/7/16

    hola amigos necesito de su ayuda , intento hacer una ecuacion pero no se como realizara , no se si habra algun video que me enseñe como hacerlo.
    es esta ecuacio
    x^6+3x^5-13x^4-25x^3+50x^2+24x=0
    de antemano mucas gracias

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 28/7/16

    Te ayudamos, Miguel:

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Antonio Silvio Palmitano
    el 28/7/16

    Para comenzar, observa que tienes factor común x en todos los términos de la izquierda (con cero a la derecha de la igualdad), por lo que una de las raíces es x = 0, luego factorizas y queda:
    x * (x^5 + 3x^4 - 13x^3 - 25x^2 + 50x + 24) =0
    que por ley de anulación del producto se descompone en dos ecuaciones:
    x = 0 (cuya raíz es cero, como ya hemos señalado)
    x^5 + 3x^4 - 13x^3 - 25x^2 + 50x + 24 = 0
    Esta nueva ecuación es la que contiene las cinco raíces que faltan, y como no es visible algún caso de factoreo, sólo queda investigar por inspección cuáles son alguna de sus raíces: puedes verificar que 2, -3 y -4 son tres raíces, ya que al evaluar todas verifican la ecuación.
    Por lo tanto, puedes dividir por medio de la regla de Ruffini en forma consecutiva al polinomio P(x) = x^5 + 3x^4 - 13x^3 - 25x^2 + 50x + 24.
    Aplicas la regla para 2 y queda el cociente:
    x^4 + 5x^3 - 3x^2 - 31x -12
    Luego aplicas la regla para -3 y queda el cociente:
    x^3 +2x^2 - 9x - 4
    Luego aplicas la regla para -4 y queda el cociente:
    x^2 - 2x - 1.
    Para obtener las raíces que faltan, puedes resolver la ecuación polinómica cuadrática:
    x^2 - 2x - 1 = 0
    y por medio de la fórmula resolvente llegas a las dos últimas raíces: 1 +V(2) y 1 - V(2).
    No dejes de mirar los videos.
    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Miguel
    el 3/8/16

    profe antonio come decimos en chile usted es seco, muchisimas gracias Dios lo bendiga

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Facundo Meier
    el 28/7/16

    Hola unicos!!. Me pueden decir por favor si encontre bien las funciones?
    La consigna e, sea h(x)=|x^2-1| encuentre las funciones f y g tal que fog=h
    Encontré f(x)=|x| y g(x)=x-1

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 28/7/16

    Es g(x)=x^2-1

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Enrique
    el 28/7/16

    En el ej 51 tengo una duda ,es que me pide bisectriz entre la recta y el eje de ordenada (x= o ) , no se como empezar a hacerlo, pido pistas principales

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/7/16

    Observa que te pide el lugar geométrico de los puntos que equidistan de dos rectas dadas, por lo que debes plantear igualdad entre las distancias de un punto genérico P(x,y) a las rectas dadas (más allá de la acotación que señalas):

    d(P,R1) = |5x + 12y - 60| / V(5^2 + 12^2) = |5x + 12y - 60| / 13, donde R1 es la recta de ecuación 5x + 12y -60 = 0,

    d(P,R2) = |x|, donde R2 es la recta de ecuación x = 0 (eje de ordenadas;

    luego igualas:

    |5x + 12y - 60| / 13 = |x|

    luego haces pasaje de divisor como factor:

    |5x + 12y - 60| = 13|x|

    luego elevas al cuadrado en ambos miembros:

    (5x + 12y - 60)^2 = (13x)^2

    Luego queda desarrollar y agrupar términos semejantes, y llegarás a una ecuación correspondiente a una hipérbola rotada.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Siker
    el 28/7/16

    Me gano este ejercicio, no puedo llegar a nada! he hecho como 10 ejercicios de polinomios con complejos pero este me supero :(
    ayudenme porfavor!

    reply•thumb_up•0 voto/s•flag
    icon

    Luis Cano
    el 28/7/16

    Si a,b∈ℝ entonces la conjugada de "x" también es raíz. Ahora solo sustituye el valor de "x" y de se conjugada en la ecuacion para obtener un sistema de 2x2 con el cual podras hallar los valores tanto de "a" como de "b".

    Para encontrar la raíz restante puedes aplicar Ruffini para factorizar dicho polinomio.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo