-
Hola como estáis? Necesito que me ayuden a resolver este ejercicio no me saleee!
Reemplazo igual a las razones trigonometricas aunque sea la letra beta?

Antonio Silvio Palmitano
el 30/7/16Primero precisemos bien la ecuación (si no es así, por favor indícalo).
3*(tanB)^2 + 5 = 7/cosB (observa que indicamos B en lugar de "beta")
Luego puedes expresar a la tangente con la identidad: tanB = senB/cosB, elevamos al cuadrado esta última expresion, reemplazamos y queda:
3 * (senB)^2 / (cosB)^2 + 5 = 7/cosB
Luego puedes multiplicar en todos los términos por (cosB)^2, simplificas en el primer término de la izquierda y en el término de la derecha y queda:
3*(senB)^2 + 5*(cosB)^2 = 7*cosB
Luego puedes sustituir (senB)^2 con la identidad trigonométrica: (senB)^2 = 1 - (cosB)^2, reemplazas y queda:
3*(1 - (cosB)^2) + 5*(cosB)^2 = 7*cosB
Luego distribuyes en el término del agrupamiento y queda:
3 - 3*(cosB)^2 + 5*(cosB)^2 = 7*cosB
Luego reduces términos semejantes a la izquierda, haces pasaje de término con el término de la derecha, ordenas términos y queda:
2*(cosB)^2 - 7*cosB + 3 = 0
Luego plantea la sustitución: w = cosB, sustituyes y queda:
2 * w^2 - 7 * w + 3 = 0
Observa que es una ecuación polinómica cuadrática, cuyas soluciones puedes obtener con la fórmula resolvente las soluciones:
w1 = 3
w2 = 1/2
Observa también, que debes considerar las soluciones cuyo valor esté comprendido entre -1 y 1, ya que w = cosB, por lo tanto nos quedamos con:
w2 = 1/2
Volvemos a la sustitución, reemplazamos y queda:
cosB = 1/2
Luego componemos con la función inversa del coseno para despejar los valores de B:
B = arccos(1/2)
Observa que tenemos dos soluciones:
B1 = pi/6 en el primer cuadrante
B2 = 5pi/6 en el segundo cuadrante.
Espero haberte ayudado. -


Antonio Silvio Palmitano
el 30/7/162a)
Para los caminos con ecuación de la forma y = mx (familia de caminos rectos que pasar por el punto de estudio (0,0))
observa que si sustituyes en la expresión de la función, ésta toma la forma:
F(x) = x / (x + mx) = x / (x(1 + m)) = 1 / (1+ m), y que el límite tendiendo a (0,0) tiende a m / (1 + m), por lo que concluimos que no existe y que, por lo tanto, la función es discontinua en (0,0), y observa que (0,0) no pertenece al dominio de la función, por lo que tienes otro motivo para justificar que no es continua en dicho punto.
Para el camino con ecuación x = 1, observa que este camino recto paralelo al eje de ordenadas no pasa por el punto (0,0), por lo que no es útil para evaluar el límite de la función tendiendo a (0,0).
En el ejercicio 2b:
observa que el dominio de la función es R^2 - {(0,0)}, por lo que ya sabemos que la función no es continua en (0,0)
observa que el numerador de la expresión se puede factorizar y la expresión queda:
f(x,y) = x*(x^2 + y^2)/(x^2 + y^2)
observa que al simplificar, la expresión queda:
f(x,y) = x
Observa que como hemos simplificado el argumento en general, esta simplificación nos sirve para estudiar el valor del límite para cualquier familia de caminos que pasen por el punto de estudio
Y observa por último que el límite queda:
Lím ((x,y)-->(0,0) f(x,y) = Lím ((x,y)-->(0,0) x = 0
Por lo que concluimos que la función es discontinua evitable en (0,0), por que puede ser redefinida como función partida:
(x^3 + x * y^2) / (x^2 + y^2) para (x,y) distinto de (0,0)
F(x,y) =
0 para (x,y) = (0,0)
y la función partida resulta continua en (0,0).
Espero haberte ayudado.
-
Consulta: ¿Cómo expreso de manera ordinaria el siguiente número escrito en notación científica?
-(4/3).10^5=
Gracias -
Necesito ayuda con la obtención de las fracciones parciales de: (x^3+6x-4)/(x-2)^3
Nosé como llegar al resultado que es: 6/(x-2)+18/(x-2)^2+16/(x-2)^3+1 , según la calculadora de fracciones parciales de wolfram. :/


Antonio Silvio Palmitano
el 29/7/16Va una orientación, a parir de la expresión fraccionaria que estás tratando.
Observa que el numerador es de grado 3, y que el denominador también es de grado 3, por lo que primero debes efectuar la división por medio del algoritmo, ahí verás que el cociente es 1, y que el resto es 6x^2 - 18x +4, por lo que la fracción puede descomponerse y queda:
1 + (6x^2 - 18x +4) / (x - 2)^3
Luego puedes aplicar la descomposición en suma de fracciones parciales para denominadores múltiples, solo para el término fraccionario, y continuar tu trabajo.
Espero haberte ayudado. -
Otra de figuras.
- Una pirámide regular tiene por base un cuadrado de 12 cm de lado. La altura es de 8cm. Calcula la apotema de la pirámide, el área lateral i el área total.
La apotema no tengo ni idea de como sacarla. Respecto lo demás he hecho lo siguiente : adjunto foto.


Antonio Silvio Palmitano
el 29/7/16Puedes recurrir a algún graficador tridimensional, y verás que la apotema de la base (su longitud es la mitad del lado de la base), la apotema de la cara lateral correspondiente (que es la altura de la cara, que es triangular) y la altura de la pirámide forman un triángulo rectángulo, cuyos elementos son:
cateto1: apotema de la base = 6
cateto2: altura de la pirámide = 8
hipótenusa: apotema de la cara lateral = x
luego, por medio de la relación pitagórica, puedes calcular la apotema de la cara lateral:
x = V(6^2 + 8^2) = V(36 + 64) = V(100) = 10.
Luego puedes pasar a calcular áreas laterales (son cuatro triángulos con iguales dimensiones: base = 12, altura = 10 (apotema de la cara), por lo tanto:
área de una cara = 12*10/2 = 60 (en unidades de área, en este caso cm^2)
Luego, como tenemos cuatro caras con iguales dimensiones: }
área de las cuaro caras = 4*60 = 240 (en cm^2)
Luego pasamos al área de la base (que has planteado correctamente):
área de la base = 12*12 = 144 (en cm^2).
Luego, para el área lateral total (contando base y todas las caras):
área lateral total = 240 + 144 = 384 (en cm^2).
Espero haberte ayudado. -
Hola a tod@s. De nuevo por aquí con geometría de 3º ESO. Un par de ejercicios. Os aseguro que antes de preguntar he buscado y rebuscado por la WEB pero no logro entender...
- Los lados de un triangulo miden 18m, 14m y 26 m. Cuanto harán los lados de un triangulo semejante de 377m de perímetro ?
- De 2 triángulos rectángulos semejantes, conocemos la longitud de los catetos del más grande, 16 cm y 24 cm, y el área del pequeño, 56cm cuadrados. Calcula cuanto hace la hipotenusa de cada uno de los 2 triángulos.
Os agradecería explicación. Ya os digo, hasta donde he podido llegar es a solucionar un ejercicio de semejanza básico, en el que debía averiguar uno de los lados de uno de los 2 triangulos, sabiendo los datos del resto. Hasta ahí sí, pero estos 2 "na de na".
Gracias de nuevo

Antonio Silvio Palmitano
el 29/7/161)
Puedes comenzar por llamar a, b y c a las longitudes del triángulo que estás buscando.
Luego, por semejanza, se cumple que:
a/18 = b/14 =c/26 = t, donde t es la constante de proporcionalidad
luego, puedes descomponer la triple igualdad:
a/18 = t, de donde tienes: a = 18t *
b/14 = t, de donde tienes: b = 14t **
c/26 = t, de donde tienes: c = 26t ***
Luego, a partir del dato del perímetro del triángulo:
a + b + c = 377
puedes sustituir y queda:
18t + 14t +26t = 377
reduces términos semejantes y queda:
58t = 377
luego haces pasaje de factor como divisor, y obtienes:
t = 377/58 = 6,5.
Por último, reemplazas en las ecuaciones que hemos señalado con asteriscos, y llegas por fin a:
a = 18*6,5 = 117
b = 14*6,5 = 91
c = 26* 6,5 = 169
que son las longitudes de los lados del triángulo, expresadas en metros.
2)
La idea a aplicar es similar a la anterior, puedes comenzar por llamar a y b las longitudes de los catetos del triángulo menor, y por semejanza puedes plantear:
a/16 = b/24 = t, de donde puedes obtener: a = 16t, b = 24t.
Luego, el área del triángulo menor es dato, y tenemos que:
ab/2 = 56
reemplazamos y queda:
16t*24t/2 = 56
resolvemos a la izquierda y queda:
192 * t^2 = 56
hacemos pasaje de factor como divisor y queda:
t^2 = 56/192
resolvemos y queda:
t^2 = 7/24
hacemos pasaje de potencia como raíz y queda:
t = V(7/24)
Luego volvemos a las expresiones de a y b en función de t y tenemos las longitudes de los catetos del triángulo menor:
a = 16 * V(7/24)
b = 24 *V(7/24)
Luego, por medio de la relación pitagórica, puedes calcular las longitudes de las hipotenusas:
H = V(16^2 + 24^2) para el triángulo mayor
h = V(a^2 + b^2) para el triángulo menor (queda que realices los cálculos).
Espero haberte ayudado. -
Buenos días para todos! Desde Argentina quiero agradecer enormemente a David y todo el equipo de Unicoos por tan magistral proyecto! Gracias a ustedes las matemáticas y la física son mi cable a tierra! Más que catedras y materias son de mi uso cotidiano! Nunca pensé que me fuera a gustar tanto las ciencias exactas! Gracias a ustedes logré más conocimiento y pude comprender temas que no entendía. Además fue el puente para conocer acerca de otras áreas de la ciencia como la astrofísica y demás! Nunca dejen de transmitirnos estos fabulosos conocimientos! Saludos!
-
Buenos dias y perdon por usar este espacio de dudas (no me va tuiter) pero simplemente quiero dar la gracias a David y a todos y cada uno de los profesores de Unicoos por la ayuda prestada en estos ultimos años.Este año he terminado 2º bachiller,he superado la Selectividad y he conseguido entrar en el grado que queria FISIOTERAPIA y algo (mucho) de todo esto os lo debo a vosotros. Mil gracias y al resto de mis compañeros de unicoos decirles "QUE SI SE PUEDE". Espero me podais seguir ayudando en un futuro. Pablo


Francisco Gutiérrez Mora
el 29/7/16Pablo, yo no sé si he tenido la oportunidad de poderte ayudar, no obstante, como asiduo colaborador en Únicoos en la tarea de contestar dudas, me alegro muchísimo de tus éxitos tanto en bachiller como en Selectividad. Enhorabuena Pablo. ¡¡¡Muchísima Suerte en la Universidad!!!. Un Saludo.
-
Ayudaa por favor, que dia de la semana sera el 25 de agosto de 2020? utilizando procedimientos matematicos..¿? graciasss


Antonio Silvio Palmitano
el 29/7/16Observa primero que el 25 de agosto de 2016 es jueves.
Luego, para llegar a la misma fecha pero en 2017 habrán pasado 365 días,
observa que para contar cuántas semanas habrán transcurrido, puedes dividir por 7 y verás que el cociente es 52 (semanas completas) y el resto es 1 (día), por lo que concluimos que el 25 de agosto de 2017 será viernes (observa que al tanscurrir semana completa tras semana completa, vamos "saltando" de jueves a jueves, por lo que el día sobrante es determinante).
Luego, para llegar a la misma fecha pero en 2018 hacemos el mismo planteo, por lo que concluimos que el 25 de agosto de 2018 será sábado.
Luego, para llegar a la misma fecha pero en 2019 hacemos el mismo planteo, por lo que concluimos que el 25 de agosto de 2019 será domingo.
Luego, para llegar a la misma fecha pero de 2020 debemos tener en cuenta que 2020 es un año bisiesto (febrero tendrá 29 días), por lo que repetimos el procedimiento pero transcurrirá un día más, por lo que concluimos que el 25 de agosto de 2020 (observa que es fecha posterior al 29 de febrero de dicho año) será martes.
Espero haberte ayudado.







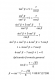


_Thumb.jpeg)










