-
Hola, saben hace mucho tiempo tengo un problema que no lo puedo resolver. Es un sistema de ecuaciones, aunque sé el resultado, lo que no entiendo es como hacer el desarrollo de este ejercicio (paso a paso si es posible)
Gracias, ojala me puedan ayudar
Muchas personas trataron de hacerlo pero nadie logra hacer el desarrollo :/ -
hola unicoos, estoy devuelta con otro problema. Ya lo he resuelto (no se si están bien los resultados alto=29m ancho=33m y precio total=3696$), pero quería saber si hay alguna manera de resolverlo mediante ecuación de la recta que pasa por un punto. Agradeceria muchisimo su ayuda


Francisco Gutiérrez Mora
el 29/7/16A ver Ana, tienes mal las dimensiones del rectángulo. El precio te sale bien porque se parte del dato dado del perímetro: te lo envío hecho:
Perímetro = 224 m;Ancho= A; Largo= L
P=2L+2A
L=(A+4)→P=2(A+4)+2A→P=2A+2A+8→P-4=4A→224-8=4A→A=216/4=54 m; L=A+4=54+4=58 m
Coste del ml alambrado =15 $→224 ml·15 $/ml=3360 $
Nº de postes=224 m/1 p/2m=112 postes. Coste de los postes= 112 p·3$/p=336 $
Coste Total = 3360+336=3696 $
Un saludo.
-
Holaa, como podria empezar hacer este ejercicio?? El dividendo de una división entera es menor que
5000. El cociente de esa división es 93 y el resto es 51.
Determina los valores posibles del dividendo y del divisor. -


Antonio Silvio Palmitano
el 29/7/16Podemos llamar x a la cantidad de artículos.
Luego, podemos plantear función costo, con expresión: C(x) = 5253 + 37x (suma de costo fijo más costo total por producir x artículos).
Luego, podemos plantear función ingreso, con expresión: Y(x) = 58x.
Y luego, podemos plantear la función utilidad, con expresión:
U(x) = Y(x) - C(x) (observa que si U(x) > 0 se obtiene ganancia, si U(x) < 0 se obtiene pérdida, y si U(x) = 0 hay equilibrio)
U(x) = 58x - (5253 + 37x)
luego, distrbuimos y queda:
U(x) = 58x - 5253 - 37x
luego reducimos términos semejantes, y obtenemos la expresión de la función utilidad:
U(x) = 21x - 5253.
Vamos ahora con las preguntas:
a)
U(141) = 21*141 - 5253 = 2961 - 5253 = -2292 <0, por lo que se registra una pérdida de$ 2292.
b)
U(x) = 4256
21x - 5253 = 4256
hacemos un pasaje de término y resolvemos:
21x = 4256 + 5253
21x = 9509
Luego terminamos de despejar con un pasaje de factor como divisor:
x = 9509/21
x = 452, 8 (aproximadamente)
Por lo que podemos responder que deberá vender como mínimo 453 artículos, para obtener una utilidad de más de $ 4256.
Espero haberte ayudado. -
Hola amigos, alguien me ayudaría hallar el rea entre x=0 y x=a, y el eje x. De la curva
ay=x(a²-y²)^(1/2).
Sol. 1/3 a^2
Gracias de antemano..

Antonio Silvio Palmitano
el 28/7/16Veamos la ecuación de la curva:
ay = x* (a^2 - y^2)^(1/2)
Observa que para x = 0 corresponde y = 0, y que para x = a corresponde y = a/V(2). Sería muy conveniente que busques un graficador para visualizar mejor la situación.
Para tratar de llegar a alguna ecuación explícita, elevamos al cuadrado en ambos miembros y distribuimos el exponente a la derecha de la iguadad y queda:
a^2 * y^2 = x^2 * (a^2 - y^2)
Luego distribuimos a la derecha de la igualdad y queda:
a^2 * y^2 = a^2 * x^2 - x^2 * y^2
Luego hacemos pasaje de término, y extraemos factor común a la izquierda y queda:
(a^2 + x^2) * y^2 = a^2 * x^2
Luego hacemos pasaje del factor (el agrupamiento, que es estrictamente positivo) como divisor y queda:
y^2 = (a^2 * x^2) / (a^2 + x^2)
Luego hacemos pasaje de potencia como raíz y llegamos a:
y = ax / V(a^2 + x^2) (observa que consideramos la opción positiva de la raíz cuadrada, y consideramos además que a > 0).
Luego, solo queda integrar la función entre 0 y a, y observa que puedes resolverla por medio de la sustitución (cambio de variable) w = a^2 + x^2.
Espero haberte ayudado. -






_Thumb.jpg)



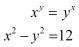



_Thumb.png)


_Thumb.jpg)
_Thumb.png)




_Thumb.jpeg)

_Thumb.jpg)

