-
Hola!
me contestaron como resolver un producto de tres matrices con la foto adjunta. Lo resuelven en dos pasos, la primera por la segunda y el resultado por la tercera en el segundo paso.
pero hay dos cosas que no entiendo:
¿De donde sale en el 1º paso (+2y+2z, -2y-2z+2z, -2y-2z+2y)?
¿por que en el 2º paso, cada producto de FxC no lo has separado por una coma al igual que en el primer paso? ¿y luego lo resuelves todo junto? -
Hola! Tengo una duda en el desarrollo de este cuadrado. No sé qué hago mal y al sustituir un número para ver si las expresiones que obtengo son equivalentes me dan resultados bastante diferentes... Agradezco la ayuda de antemano :)
-
Hola Unicoos!!. Me pueden ayudar por favor con ejercicio a, la consigna es analizar concavidad y determinar si poseen puntos de inflexión.
He visto sus vídeos, pero sigo sin entender
Muchas gracias

Antonio Silvio Palmitano
el 25/7/16Primero comencemos por repasar el criterio para analizar concavidad:
f tendrá gráfica cóncava hacia arriba en un punto de su dominio cuando f '' (xo) > 0,
f tendrá gráfica cóncava hacia abajo en un punto de su dominio cuando f ' ' (xo) < 0,
y se deberán analizar como posibles inflexiones cuando f ' ' (xo) no esté definida, y también cuando f' ' (xo) = 0.
a) La función tiene dominio R, y su derivada segunda queda:
f ' ' (x) = 6x - 2, luego igualas a cero, despejas y obtienes: x1 = 1/3,
luego puedes evaluar la derivada segunda para un valor menor, y para otro valor mayor que 1/3:
f ' ' (0) = - 2 < 0, por lo que la gráfica es cóncava hacia abajo en (-inf ; 1/3),
f ' ' (1) = 4 > 0, por lo que la gráfica es cóncava hacia arriba en (1/3 ; +inf),
por lo que concluimos que la gráfica presenta una inflexión en x1 = 1/3.
Observa que para la función polinómica que hemos tratado, el dominio de la función, el de su derivada primera y de su derivada segunda es el conjunto de los números reales.
b)
Observa que el dominio de la función es el conjunto de los números reales (el denominador de la expresión es estrictamente mayor que cero).
Plantea su derivada primera: f ' (x) = -2x / (x^2 + 3)^2, que existe en todo el dominio de la función, luego
plantea su derivada segunda: f ''= (6*x^2 - 6) / (x^2 + 3)^3, que existe en todo el dominio de la función.
Luego plantea la condición de posible inflexión:
f ' ' (x) = 0
luego despejas, y obtienes dos valores: x1 = -1, y también x2 = 1.
Luego puedes proceder como en el ejercicio anterior y evaluara la derivada segunda para valores anterior, intermedio y posterior a los indicados, por ejemplo:
f '' (-2) = 18 / 343 > 0, por lo que la gráfica es cóncava hacia arriba,
f ' ' (0) = -6 / 27 < 0, por lo que gráfica es cóncava hacia abajo,
y la gráfica de la función presenta inflexión en x1 = -1.
Luego repetimos el procedimiento para x2 = 1 (observa que la evaluación que ya hicimos en 0 nos es útil):
f ' ' (2) = 18 / 343 > 0, por lo que la gráfica es cóncava hacia arriba,
y la gráfica de la función presenta inflexión en x2 = 1.
c)
Observa que la función tiene dominio R, y que es continua en todo su dominio,
luego plantea su derivada primera (observa que no está definida para el punto de pegado entre trozos x1 = 2):
2x x < 2
f ' (x) = no está definida x = 2
-2x x > 2
luego plantea su derivada segunda, y observa que no está definida en x1 = 2:
2 x < 2
f ' (x) = no está definida x = 2
-2 x > 2
Observa que la gráfica de la función es:
cóncava hacia arriba en (-inf ; 2),
cóncava hacia abajo en (2 ; +inf,
por lo que concluimos que la gráfica presenta una inflexión en x1 = 2.
-
Unicoos & algún usuario que pueda ayudarme:
Estoy intentando aprender las nociones teóricas del calculo esencial, y pude comprender las demostraciones de los conceptos de límites, derivadas, etc.
Sin embargo me queda un cabo suelto acerca de lo que es un diferencial.
Específicamente, me refiero a que no sé que es la variable "dy" y "dx" en la formula f(x) = dy/dx
¿representa dy/dx la razón de cambio de la función f(x)?
Disculpe las molestias. -
Hola Unicoos!
Me ayudan a resolver esas dos integrales? Sé que ambas deben darme arctg(e^x)+c, pero no hay forma que llegue. La integral debería quedarme como una fracción con la derivada de u en el numerador y 1+u^2 en el denominador, pero no hay caso.
Desde ya, gracias!
jorge velazquez
el 25/7/16Profesor me parece con todo Redpeto a su Labor, que No es necesario el cambio de variable, se puede escribir e^2x como (e^x)^2 y de esta forma el proceso es el mismo, y por ende, sólo tiene que hacer uso del modelo, lo digo de esta forma para que no sea más dispendioso el ejercicio para Vale.
Reitero solo es por ese motivo por el contrario, sería otra manera de resolverlo.
Valeria
el 25/7/16Muchas gracias a todos!
Así es, especificaba el resultado, por lo tanto, podía llegar a suponer cuál era la regla que debía usar. Una consulta con respecto a la resolución:
Antonio, ¿Cómo lograste escribir esa parte, es decir, pasar de la división a la multiplicación? Entiendo que la propiedad A/B/C/D=AxD/BxC no me sirve para que quede así -
Hace rato pregunte algo y me pidio que subiera la foto del enunciado por eso repido la pregunta no es spam
Es el numero 7 con el que tengo duda.
en las instrucciones solo dice : comprobar la identidad de las siguientes ecuaciones.


Andrés Alvarado
el 25/7/16Pues... Primeramente se trata de partir de la izquierda y llegar a la expresión de la derecha o viceversa para comprobar la identidad.
En la primera línea pase todo a senos y cosenos y fui resolviendo la expresión
En la tercera línea cambio de signo el denominador por lo tanto pongo un menos al frente de la fracción y a todo multiplicó por esa expresión que no se altera debido a que es como multiplicar por uno
En la cuarta línea hice propiedad distributiva
En la quinta línea hice factor común seno de A y también factor común coseno de A y mi denominador se transforma en Coseno de 2A
En la sexta línea hice factor común (1-senAcosA) y el denominador cambia por identidad.
En la segunda línea de la segunda foto hago valer a 1 como seno al cuadrado más coseno al cuadrado y el signo de la fracción la pasó al denominador.
Y listo, suerte :) saludos... -
Hola, queria saber si me podian ayudar con este problema de funciones trigonometricas. la maestra lo estaba explicando y no pudo resolverlo porque no se acordaba de que era = tgA - 1 y en lo que revisaba para recordar se acabo la clase y ya no lo hizo.
sec A - senA / tgA - 1 = sen^3 A + cos^3 A / 1 - 2cos^2 A -
Hola, unicoos! Podrían ayudarme con este ejercicio? Estuve viendo los videos de combinatoria, pero aun así me cuesta un poco resolverlo.. Ahí va:
En un estante hay 6 botellas de vodka, 8 de licor y de 10 de jugo. De cuantas maneras se las puede acomodar si
a) las botellas de una misma clase deben quedar juntas?
b) sólo se quiere que las de jugo queden juntas?
Sé que para cada grupo de botellas tengo que sacar su factorial para saber las combinaciones posibles, pero no se qué tengo que hacer para agruparlas.
En el a) quise hacer 6!+8!+10! pero cómo reflejo que los grupos de botellas no se mezclen entre sí?
Desde ya muchas gracias!!

Antonio Silvio Palmitano
el 25/7/16Vamos con tus preguntas.
a)
Ordenas primero por clase de bebidas: 3! = 6 posibilidades.
Luego, por cada uno de esos seis ordenamientos tienes 6! ordenamientos de la botellas de vodka, y por cada uno de ellos tienes 8! ordenamientos de las botellas de licor, y por cada uno de ellos tienes 10! ordenamientos posibles de las botellas de jugo, por tanto puedes aplicar el el principio de multiplicación: N = 3!*6!*8!*10!
b)
Observa que la cantidad total de botellas a ordenar es 24, y que las botellas de jugo pueden ocupar los lugares: 1 al 10, o 2 al 11, o 3 al 12, o ... 15 al 24, lo que totalizan 15 posibilidades, y por cada una de ellas tienes 10! ordenamientos de las botellas de jugo y, para el resto (que son 14 en total) tienes 14! ordenamientos posibles, por tanto la cantidad de maneras posibles es: M = 15*10!*14!.
Espero haberte ayudado.
Barbara Ferrari
el 25/7/16Si, parece que no estaba tan perdida entonces, entendí lo que hay que hacer pero en el b) no hay una manera mas sencilla de calcularlo? Porque yo lo traté de hacer a mano justamente porque me di cuenta que las botellas podian estar ubicadas de varias formas, pero solo así podia darme cuenta de la cantidad de combinaciones posibles para ordenarlas, no?





_Thumb.jpg)




_Thumb.jpeg)

_Thumb.jpg)
_Thumb.png)

_Thumb.jpg)
_Thumb.png)

_Thumb.jpg)

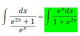





_Thumb.jpg)

_Thumb.jpg)

_Thumb.jpeg)

_Thumb.jpeg)

_Thumb.jpeg)



_Thumb.jpg)
