-
Hola Unicoos!! Alguien que sepa aclararme la duda para integral por método de sustitución trigonometrica...
Mi duda pasa por ese 4 delante de x²
porque tengo entendido que hay tres casos y una de ella es esta expresión (x² -a)½ -
Hola, tengo otra duda con encontrar el area entre funciones. Me dan dos funciones, despejo la "y" en ambas, y me da +-raiz de 2-x. No se cual de las dos soluciones tomar, si el positivo o el negativo.


Antonio Silvio Palmitano
el 25/7/16Puedes también optar por despejar x en ambas ecuaciones, e integrar luego con respecto a la variable y.
Las ecuaciones quedan.
x = 2 - y^2 (observa que corresponde a una parábola con vértice en el punto de coordeenadas (2,0), cuyas ramas se abren hacia el semieje x negativo)
x = -y (observa que se trata de la recta bisectriz del segundo y del cuarto cuadrante)
A esta altura es muy conveniente hacer un gráfico, y verás que la región está limitada "por la izquierda" por la recta, y "por la derecha" por la parábola), por lo que la función a integrar para calcular el área de la región queda:
(2 - y^2) - (-y) = 2 - y^2 + y
Luego, para determinar los límites de integración, igualamos ambas ecuaciones y tenemos:
-y =2 - y^2, pasamos términos y queda:
y^2 - y - 2 = 0, cuyas soluciones son y = - 1 e y = 2 (observa que los puntos de intersección tienen coordenadas (1 , -1) y (-2 , 2)), y como estamos integrando con respecto a y, el intervalo de integración queda: -1 <= y <= 2.
Observa que integrar con respecto a y es un buen recurso en casos como el que nos ocupa en este caso.
Espero haberte ayudado. -
Tengo una duda de deribada, aca les dejo la consigna, mi duda es con lo que me piden, tengo que verificar que la funcion pase por el origen? o tengo que integrar y verifcar que paso por el origen la funcion que integre?]
pd: no subi la foto del procedimiento entero. pero me quedo asi. disculpen la desproligidad pero no tengo demaciado tiempo T_T -
Hola unicoos, ¿Podrían ayudarme con este problema?: El 70% de los alumnos de una clase universitaria han aprobado un examen; la séptima parte de los aprobados ha obtenido sobresaliente sobresaliente. Si los sobresalientes son 7, ¿cuantos alumnos hay en la clase?.
Llevo mal los problemas con datos con porcentajes, agradecería una explicación que me ayude a resolverlos. Muchas gracias de antemano.
Julian Jerez
el 24/7/16Primero utilizas el dato que la septima parte de los sobresalientes son 7, y haces que 1/7x=7, que quiere decir que un septimo de x es 7. Averiguamos cuanto es x y da que x= 49. Ya sabemos que el 70% de los alumnos es 49. Podemos hacer una regla de 3, si 49 alumnos son el 70%, cuantos son el 100%. Obtenemos que el total de alumnos son 70.
-
-
Hola otra vez, ¿podrían ayudarme en el siguiente ejercicio? Si sabéis algún vídeo que explique el ejercicio no estaría nada mal, a no ser que me lo expliquéis...


Antonio Silvio Palmitano
el 24/7/16Vamos ejercicio por ejercicio, con algunas orientaciones: a veces es conveniente investigar raíces (llamemos a a una de ellas)y, al encontrarlas, dividir por el factor elemental correspondiente (x -a) para poder factorizarlo y, en otras ocasiones, resulta más conveniente aplicar algún caso de factorización, o la fórmula resolvente para ecuaciones polinómicas de grado dos.
1)
en el numerador puedes aplicar la sustitución u = x^2, te quedará: 2 + 3u+ u^2 = (u +1)(u+2) = (x^2 + 1)(x^2 + 2),
en el denominador puedes factorizar por grupos: 1(-1 + x) + x^2 * (-1 + x) = (1 + x^2)(-1 + x),
luego, observa que comparten un factor, que podrás simplificar al reemplazar en la expresión fraccionaria.
2)
en el numerador puedes emplear la fórmula resolvente,
en el denominador puedes aplicar diferencia de cuadrados (observa que en uno de los factores lo podrás hacer otra vez),
luego podrás simplificar factores compartidos al sustituir en la expresión fraccionaria
3)
en el numerador observa que 1 es una raíz, por lo que puedes dividir por (x - 1) para luego factorizar,
en el denominador puedes extraer factor común y queda. x(10 + 3x - 6x^2 + x^3), y observa también que en el agrupamiento -1 es una raíz, por lo que puedes dividir por (x +1) para luego factorizar,
y como venimos haciendo, sustituyes luego en la expresión fraccionaria y simplificarás si encuentras factores compartidos.
4)
en el numerador observa que 2 es una raíz, por lo que puedes dividir por (x - 2) para luego factorizar,
en el denominador puedes extraer factor común por grupos: 9(-1 + x) - 10x^2 * (-1 + x) + x^4 * (-1 + x) =(-1 + x)(9 -10x^2 + x^4), y luego puedes emplear para el agrupamiento mayor el mismo procedimiento que empleamos con el numerador en el primer ejercicio.
Es muy aconsejable realizar los cálculos auxiliares en un sector aparte del ejercicio, y una vez factorizado, también revisar si es posible volver a factorizar en los agrupamientos.
Espero haberte ayudado.


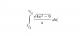

_Thumb.jpg)

_Thumb.jpg)

_Thumb.jpg)

_Thumb.jpg)


_Thumb.jpg)


_Thumb.jpg)


_Thumb.jpg)





_Thumb.jpg)




_Thumb.jpg)

_Thumb.jpg)

_Thumb.jpg)


_Thumb.jpg)

_Thumb.jpg)



_Thumb.jpg)




