-
Y3
el 25/1/20 -
German
el 25/1/20Tengo que hallar la intersección entre estas dos ecuaciones. Por favor me podrían ayudar?
f(x)=ex
g(x)=X3
¿Esta bien igualarlas? Si es así desde acá no se como seguir, intente aplicar logaritmo a ambos lados pero no se si es lo correcto.
ex = X3
ln ex = ln X3
x ln (e)= 3 ln(x)
x.1= 3 ln(x)
x=3ln(x) -------------------> y hasta ahi llegue no se como despejar X
-
Ignasi
el 25/1/20Hola! Ahí va un nuevo ejercicio. Este problema lo hicieron en un concurso llamado "Copa Cangur" en 2015 estudiantes de segundo y tercero de ESO. ¿Alguien sabría como resolverlo? Es el siguiente:
¿De cuántas formas puedo cambiar una moneda de 0,50€ con monedas de 0,20€, 0,05€, 0,02€ y/o 0,01€?
Saludos a todos y gracias!
-
Juan Romero Herraiz
el 25/1/20
-
Lara
el 25/1/20Hola buenas alguien me podría ayudar a resolver este problema con conceptos de trigonometria y vectores ( punto medio, longitud de la mediana,tangentes...) ? :
Calcula el área y los ángulos del triángulo con vértices A ( -5,-2) B(3,-1) y C (1,4).
Gracias.
-
Y3
el 25/1/20 -
Y3
el 25/1/20
Alguien me ayuda con un dibujo de esto porfa? Gracias!
Breaking Vlad
hace 3 semanas, 6 díasse trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
carmela
el 25/1/20 -
Y3
el 25/1/20
Alguien me podría guiar un poco con este ejercicio? No lo pillo. Gracias!
Jose Ramos
el 25/1/20Para que tres vectores sean linealmente dependientes, puedes hacer lo siguiente:
a) ver que el rango de la matriz que forman es menor que 3 (si es 3 serían linealmente independientes)
b) Intentar escribir uno de ellos en combinación lineal de los otros dos (si lo logras serían dependientes).
Te hago el ejercicio de las dos maneras:
-
Y3
el 25/1/20
No entiendo por qué podemos aplicar esta fórmula (ver amarillo) si es vector director de s no es paralelo al plano.
Jose Ramos
el 25/1/20
Y3
el 25/1/20
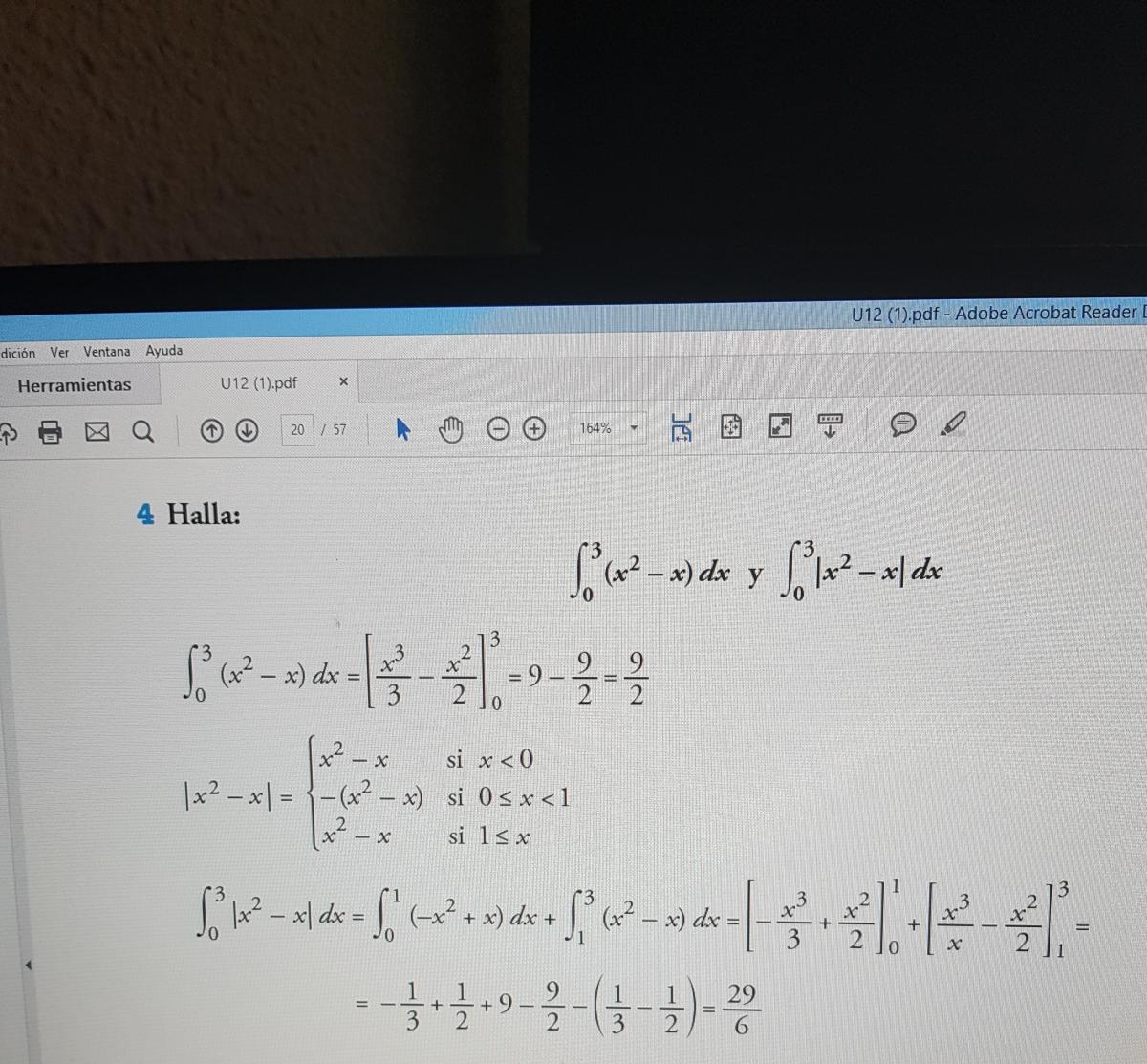Buenos días. Alguien me puede explicar la forma de desglosar el valor absoluto en intervalos? No entiendo ente 0 y 1. Mil gracias
