-
Hola, mi consulta es como hacer este tipo de problemas, cual es la teoría necesaria para encararlos? porque no se como se hacen ninguno de ellos!


David
el 30/4/16No hace falta teoría. _El enunciado te lo dice todo... Sustituye chx y shx en ch²x-sh²x=1...
Te quedará (e^x+e^(-x))²/4 - (e^x-e^(-x))²/4 = [e^(2x)+e^(-2x) +2.e^x.e^(-x) - e^(2x)-e^(-2x)+2.e^x.e^(-x) ]/4 = 4.e^x.e^(-x)/4 =e^x.e^(-x) = e^(x-x)=e^0=1....
¿mejor?... Para el resto, lo mismo.. Aplicar despues identidades notables, mutliplicacion de potencias de la misma base, etc, etc... ANIMO!
Para la b) y la c) deberás derivar las expresiones (e^x+e^(-x))/2 o (e^x-e^(-x))/2 .. ¿sabes derivar bien?...
si sigues con dudas, lo ideal es que nos envíes que conseguiste, paso a paso, esté bien o mal...... -
Podríais ayudarme con estos dos ejercicios de optimización? No sé sacar la relación que tienen los datos que me dan.
-


David
el 30/4/16Son integrales de tipo arcotangente... Te sugiero este video, al menos.. Integrales inmediatas y definidas
Se pueden hacer tambien por cambio de variable..
Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok? -
No sé cómo debo resolver este sistema. Lo he intentado de dos maneras distintas. Las dos ecuaciones son dependientes, pero al intentar resolverla por segunda vez, me sale indeterminación: 0y, 0z






_Thumb.jpg)




_Thumb.png)









_Thumb.jpg)




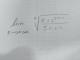



_Thumb.jpg)

