Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

María
el 30/4/16

Hola,
Creen que esta bien hecha esta ecuación diferencial de primer orden homogénea?
Gracias
••0 voto/s
•
César
el 30/4/16
Has tenido un fallo en las operaciones
•1 voto/s
•

Cancelar
Nacho
el 30/4/16

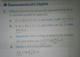
no entiendo como resolver este ejercicio de complejos, me pasa siepre que tengo el complejo elevado a numeros "grandes"..

si alguien me puede dar una mano con este ejercicio, y pasarme la forma general para resolverlos o la "receta"
gracias!!!!!!!!!

si alguien me puede dar una mano con este ejercicio, y pasarme la forma general para resolverlos o la "receta"
gracias!!!!!!!!!">
••0 voto/s
•
David
el 30/4/16
Pasalo a forma polar y elevalo a 16.... ¿lo intentaste?... ¿has visto estos videos?... Numeros complejos 03 - De forma binomica a polar Numeros complejos 01 - Operaciones en forma polar
Como i+i en forma polar es √2, 45º.... (1+i)√2/2= (√2, 45º).√2/2 = (√2.√2/2 , 45º)=1,45º...
Si lo elevas a 16 te quedará 1, 45.16=1, 720º=1, 360º = 1
•0 voto/s
•
Antonius Benedictus
el 30/4/16
Te explicamos, Nacho:
•0 voto/s
•

Cancelar
Salomé
el 30/4/16

Hola buenos días, podríais ayudarme ?

••0 voto/s
•
David
el 30/4/16
Por propiedades de los logaritmos (echales un vistazo.. Logaritmos )... log(a.b)=loga + logb..
Por tanto Ln(2^x. e . (x/3).. si está bien copiado, claro... sería Ln(2^x) + lne + Ln(x/3)= x.ln2 + 1 + Lnx - Ln3...
Y ahora integra, por separado.. Te quedará ∫ x.ln2.dx+ ∫1.dx + ∫Lnx.dx -∫Ln3.dx = ln2 . x²/2 + x + x.Ln3 + ∫Lnx.dx
Esta ultima la tienes en video... Integral por partes 02
•0 voto/s
•

Cancelar
Miquel Martos Doroteo
el 30/4/16

Hola de nuevo, tengo dudas al intentar resolver este ejercicio. La verdad es que no se como cogerlo.

¿Cuál sería la mejor manera para resolverlo? Yo pienso que tiene relación con los productos escalares y vectoriales, pero no se como llegar hasta ahí.

¡Muchas gracias por su tiempo! Les estoy muy agradecido.
••0 voto/s
•
Alba
el 30/4/16
Creo que este vídeo te puede ayudar Vectores Paralelos o perpendiculares - Producto Escalar
•0 voto/s
•
Alba
el 30/4/16
Simplemente para que dos rectas sean paralelas , los vectores tienen que ser iguales,
De ahí sacarás el valor a, ( tienes que conseguir el vector director de la segunda recta)- se hace haciendo el producto vectorial de los vectores de los dos planos
•0 voto/s
•
Alba
el 30/4/16
Haces una triple igualación: la primera coordenada del vector de la primera recta entre la primera coordenada del vector de la segunda recta igual a la segunda coordenada del vector de la primera recta entre... y así
•0 voto/s
•
Alba
el 30/4/16
todo esto es para que sean paralelas
•0 voto/s
•
Antonius Benedictus
el 30/4/16
Va, Miquel:
•1 voto/s
•

Cancelar
Alba
el 30/4/16

Holaa me podríais ayudar con este ejercicio? Me vi el video de integrales ciclicas pero me da 0, no se en que fallé exactamente, muchas gracias a todos!!!!

••0 voto/s
•
Antonius Benedictus
el 30/4/16
Te lo corregimos, Alba:
•0 voto/s
•

Cancelar
Miquel Martos Doroteo
el 30/4/16

¡Muy buenos días a todos! Me gustaría saber si he resuelto bien este ejercicio, y me gustaría que me dijesen si hay otra forma para realizar este ejercicio, ya que creo que hay más de una.

El ejercicio me pide que encuentre los valores de m y de n para que se cumpla que la recta r y el plano p sean paralelos. Yo he hecho el razonamiento por rangos: una recta será paralela a un plano cuando el rango de la matriz de coeficientes sea distinto del rango de la matriz ampliada, por ejemplo: Rg(A) = 2 y Rg(A*) = 3.

Creo que lo he hecho bien, ya que cuando determino el vector director de la recta y realizo el producto escalar con el normal asociado al plano, este me da 0.

¡Muchas gracias por la ayuda!
••0 voto/s
•
Antonius Benedictus
el 30/4/16
Te corregimos, Miquel:
•1 voto/s
•
Miquel Martos Doroteo
el 1/5/16
Buenos días Antonio, no entiendo el razonamiento que haces cuando pones: n(3-m)=1 → Rg(A)=2. ¿Me lo podrías explicar por favor?

Muchas gracias por tu tiempo :)
•0 voto/s
•

Cancelar
Sebástian
el 30/4/16

Hola chicos tengan buen día, aquí estoy con un ejercicio del teorema de comprensión si me ayudan ma harian un gran favor ayudandome. Un saludo a ustedes y muchas gracias de antemano x su contribución!
••0 voto/s
•
Antonius Benedictus
el 30/4/16
Te ayudamos, sebastián:
•0 voto/s
•

Cancelar
David
el 30/4/16

Hola! Aquí estoy de nuevo con otro ejercicio, solo sería el apartado C para saber como se resuelve. Un saludo, gracias!
••0 voto/s
•
Antonius Benedictus
el 30/4/16
Te van los tres primeros David. El c) sale 0, pues, en una variable continua, los valores sueltos no tienen probabilidad.
•1 voto/s
•
David
el 2/5/16
Perfecto, muchísimas gracias de nuevo por la ayuda. Un saludo!
•0 voto/s
•

Cancelar
Sandy Murillo S...
el 30/4/16

Hola nuevamente amigos de unicoos, les pido ayuda con el ejercicio adjunto en la imagen, necesito que me digan si esta bien o si esta mal, en caso de estar mal hagan el favor de corregirme. Vale ¡ . Y muchisisisismas gracias amigos míos y saludos a la distancia. Saludos y suerte
••0 voto/s
•
Antonius Benedictus
el 30/4/16
En x=2, el límites es 0+2=2
Y en x=1, f carece de límite.
Lo demás está bien.
•0 voto/s
•

Cancelar