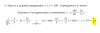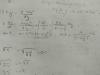-
-

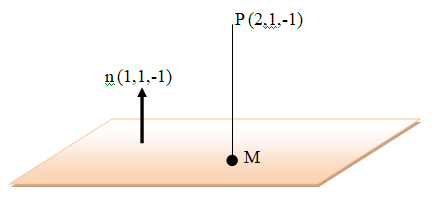
 una consulta jose ramos,Supongo que en el ejercicio a,has tomado un valor aleatorio del plano,para restarlo con el punto p y asi obtener el vector director,si es correcto, quisiera saber que valor elegiste ya que creo que no existe el que has elegido,si es que es valido lo que digo,saludos cordiales.
una consulta jose ramos,Supongo que en el ejercicio a,has tomado un valor aleatorio del plano,para restarlo con el punto p y asi obtener el vector director,si es correcto, quisiera saber que valor elegiste ya que creo que no existe el que has elegido,si es que es valido lo que digo,saludos cordiales.

Jose Ramos
el 18/1/20Pretendo hallar la recta perpendicular al plano dado y que pasa por el punto dado (2, 1,-1) obteniendo X=(2,1,-1)+λ(1,1,-1), por lo tanto no tomo ningún valor aleatorio del plano, pues el vector director de la recta viene determinado por el normal del plano. Una vez obtenida r, la interseco con el plano y ya me da directamente el punto que estoy buscando.
-
La derivada de y=Ae^t+Bte^t - e^-t
Es y'= Ae^t +Be^t + Bte^t +e^-t;
y'=Ae^t+2B(e^t+te^t)+e^-t
Esta bien??
-
 4ºESO Sistema de dos inecuaciones con una incógnita.
4ºESO Sistema de dos inecuaciones con una incógnita.Por favor ¿le echáis un vistazo al adjunto ejercicio? Creo que está bien representado gráficamente, pero tengo una pequeña duda de si en la solución (intersección de los dos intervalos) debo, o no, utilizar el símbolo ∩. Gracias por vuestra tiempo.
-
Hola, en esta ecuación diferencial de 2 orden no entiendo (punto 4) como sacar la derivada y como sacar el dato inicial a partir de esta (y'=0) por favor alguien me puede guiar. Gracias.



Antonio Silvio Palmitano
el 18/1/20Has planteado correctamente la solución de la ecuación homogénea asociada y la solución particular, y la expresión de la solución general de la ecuación diferencial te ha quedado:
y = C1*et + C2*t*et - e-t (1).
Luego, planteas la expresión de la función derivada primera (observa que debes aplicar la Regla de la Multiplicación de funciones en el segundo término), y queda:
y' = C1*et + C2*et + C2*t*et + e-t (2).
Luego, planteas la expresión de la función derivada segunda (observa que debes aplicar la Regla de la Multiplicación de funciones en el tercer término), y queda:
y'' = C1*et + C2*et + C2*et + C2*t*et - e-t, reduces términos semejantes, y queda:
y'' = C1*et + 2*C2*et + C2*t*et - e-t (3).
Luego, a partir de la primera condición inicial que tienes en tu enunciado: y(0) = 1 tienes los valores: t = 0, y = 1, los reemplazas en la ecuación señalada (1), resuelves factores en los coeficientes, y queda:
1 = c1*1 + c2*0*1 - 1, resuelves coeficientes, cancelas el término nulo, y queda:
1 = C1 - 1, y de aquí despejas: C1 = 2.
Luego, a partir de la segunda condición inicial que tienes en tu enunciado: y'(0) = 2 tienes los valores: t = 0, y' = 1, los reemplazas en la ecuación señalada (2), resuelves factores en los coeficientes, y queda:
y' = C1*1 + C2*1 + C2*0*1 + 1, resuelves coeficientes, cancelas el término nulo, y queda:
2 = C1 + C2 + 1, y de aquí despejas:
C2 = 1 - C1, reemplazas el valor que tienes remarcado, resuelves, y queda:
C2 = -1.
Luego, reemplazas los valores particulares de las constantes de integración que tienes remarcados en las expresiones señaladas (1) (2) (3), reduces términos semejantes cuando corresponda, y queda:
y = 2*et - t*et - e-t, que es la expresión de la solución particular de la ecuación diferencial de tu enunciado para las condiciones iniciales indicadas;
y' = et - t*et + e-t, que es la expresión de la derivada primera de la solución particular,
y'' = -t*et - e-t, que es la expresión de la derivada segunda de la solución particular.
Luego, puedes sustituir las expresiones de la solución particular que tienes remarcada, y las expresiones de su derivada primera y de su derivada segunda, en la ecuación diferencial de tu enunciado, a fin de verificar su validez.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 18/1/20Observa que tienes en tu enunciado que los puntos pertenecientes al lugar geométrico equidistan de un punto (en este caso el polo), y de una recta, por lo que tienes que dicho lugar geométrico es una parábola.
Tienes las coordenadas polares del punto de corte entre la recta (r) y la extensión del eje polar: A(-3,0°).
Planteas la expresión polar de un punto genérico perteneciente al lugar geométrico; P(r,θ).
Luego, planteas la expresión de la distancia entre el polo y el punto genérico, y queda:
dist(OP) = r (1).
Luego, planteas la expresión polar del punto que es la proyección del punto genérico sobre el eje polar: P1(r*cosθ,0°);
luego, observa que la distancia entre el punto genérico y la recta a la que refiere tu enunciado es igual a la distancia entre el punto A y el punto P1, por lo que puedes plantear para la expresión de la distancia entre el punto genérico y la recta:
dist(r,P) = dist(r,P1) = r*cosθ - (-3) = r*cosθ + 3 (2).
Luego, planteas la condición que cumplen los puntos pertenecientes al lugar geométrico que tienes en tu enunciado, y queda la ecuación:
dist(OP) = dist(r,P),
sustituyes la expresión señalada (1) en el primer miembro, sustituyes la expresión señalada (2) en el segundo miembro, y queda:
r = r*cosθ + 3, restas r*cosθ en ambos miembros, y queda:
r - r*cosθ = 3, extraes factor común en el primer miembro, y queda:
r*(1 - cosθ) = 3, que es una ecuación polar implícita del lugar geométrico al que refiere tu enunciado;
luego, divides en ambos miembros por (1 - cosθ) en ambos miembros, y queda:
r = 3/(1 - cosθ), que es una ecuación polar explícita del lugar geométrico al que refiere tu enunciado, con la condición: θ ≠ 0.
Espero haberte ayudado.