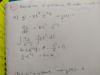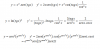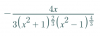-


Antonio Silvio Palmitano
el 17/1/20Tienes la ecuación diferencial:
y' = 8*t3*e-2*y (1),
con la condición inicial:
y(1) = 0 (2).
Expresas al primer miembro de la ecuación señalada (1) como cociente entre diferenciales, aplicas la propiedad de las potencias con exponente negativo en el último factor del segundo miembro, y queda:
dy/dt = 8*t3/e2*y,
separas variables, y queda:
e2*y*dy = 8*t3*dt,
multiplicas por 2 en ambos miembros, y queda:
2*e2*y*dy = 16*t3*dt,
integras en ambos miembros, y queda:
e2*y = 4*t4 + C (3),
que es la solución general de la ecuación diferencial de tu enunciado, presentada en forma implícita.
Luego, a partir de la condición inicial señalada (2) tienes los valores: t = 1, y = 0, los reemplazas en la ecuación señalada (3), y queda:
e2*0 = 4*14 + C, resuelves términos numéricos, y queda:
1 = 4 + C, restas 4 en ambos miembros, y luego despejas:
C = -3, que es el valor particular de la constante de integración para la condición inicial de tu enunciado;
luego, reemplazas este último valor en la ecuación señalada (3), y queda:
e2*y = 4*t4 - 3, compones en ambos miembros con la función inversa de la función exponencial natural, y queda:
2*y = ln(4*t4 - 3), multiplicas por 1/2 en ambos miembros, y queda:
y = (1/2)*ln(4*t4 - 3),
que es la expresión explícita de la solución particular de la ecuación diferencial de tu enunciado, con la condición inicial indicada en el mismo,
y observa que se debe cumplir la condición:
4*t4 - 3 > 0.
y puedes verificar la validez de la misma (te dejo la tarea de plantear la expresión de la función derivada, y de sustituir expresiones en la ecuación diferencial de tu enunciado).
Espero haberte ayudado.
-

 quisieea saber si esta bien,y si esta bien el analisis, el vector director lo puedo obtener haciendo el producto vectorial de ambas normales o que z=λ. Tengo una duda con el punto de paso,puedo usar el concepto de grados de libertad, x=1 asi que cuando tengo (x,5-λ,λ) en la coordenada x es 1,no es 0, eso es correcto?.desde ya gracias.
quisieea saber si esta bien,y si esta bien el analisis, el vector director lo puedo obtener haciendo el producto vectorial de ambas normales o que z=λ. Tengo una duda con el punto de paso,puedo usar el concepto de grados de libertad, x=1 asi que cuando tengo (x,5-λ,λ) en la coordenada x es 1,no es 0, eso es correcto?.desde ya gracias.


Antonio Silvio Palmitano
el 17/1/20Has resuelto bien el problema, pero te ha quedado confuso el desarrollo de tu tarea.
Has planteado y determinado correctamente la expresión de un vector director de la recta buscada, y te ha quedado:
u = < 0 ; -1 ; 1 >.
Luego, con el punto conocido de la recta buscada: M(1,5,4) y la expresión del vector director, planteas una ecuación vectorial paramétrica de la recta buscada, y queda:
< 1 ; 5 ; 4 > - < x ; y ; z > = λ*< 0 ; -1 ; 1 > (1), con λ ∈ R.
Luego, tienes la expresión planteada de un segundo punto perteneciente a la recta buscada: N(1,a,2), sustituyes sus coordenadas en el primer término de la ecuación vectorial señalad (1), y queda:
< 1 ; 5 ; 4 > - < 1 ; a ; 2 > = λ*< 0 ; -1 ; 1 >,
resuelves la resta vectorial en el primer miembro, resuelves la multiplicación de escalar por vector en el segundo miembro, y queda:
< 0 ; 5-a ; 2 > = < 0 ; -λ ; λ >;
luego, por igualdad entre expresiones vectoriales, igualas componente a componente, y queda:
0 = 0, que es una Identidad Verdadera,
5 - a = -λ, de aquí despejas: a = 5 + λ (2),
2 = λ;
luego, reemplazas el valor del parámetro que tienes remarcado en la ecuación señalada (2), resuelves, y queda:
a = 7.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 17/1/20Has separado variables, y te ha quedado la ecuación:
(1/t)*dt = [8*y/(1 - 2*y2)]*dy,
extraes factor numérico -2 en el segundo miembro, y queda:
(1/t)*dt = -2*[-4*y/(1 - 2*y2)]*dy,
integras en ambos miembros, y queda:
ln(t) + C = -2*ln(1 - 2*y2),
expresas a la constante C como el logaritmo de otra constante positiva, aplicas la propiedad del logaritmo de una potencia en el segundo miembro, y queda:
ln(t) + ln(k) = ln[(1 - 2*y2)-2], con k ∈ R, k > 0;
luego, aplicas la propiedad del logaritmo de una multiplicación en el primer miembro, y queda:
ln(k*t) = ln[(1 - 2*y2)-2],
compones en ambos miembros con la función inversa de la función logarítmica natural, y queda:
k*t = (1 - 2*y2)-2, con k ∈ R, k > 0,
que es una ecuación implícita que permite definir a la función solución general de la ecuación diferencial de tu enunciado en forma implícita.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 17/1/20Has separado correctamente las variables, y te ha quedado la ecuación diferencial:
y2*dy = (t2 - 1)*dt,
integral en ambos miembros (observa que debes corregir tu primer miembro), y queda:
y3/3 = t3/3 - t + C,
multiplicas por 3 en todos los términos de esta ecuación, y queda:
y3 = t3 - 3*t + 3*C,
expresas al último término como una nueva constante, y queda:
y3 = t3 - 3*t + k, con k ∈ R;
luego, extraes raíz cúbica en ambos miembros, y queda:
y = ∛(t3 - 3*t + k), con k ∈ R,
que es la expresión explícita de la solución general de la ecuación diferencial de tu enunciado.
Espero haberte ayudado.