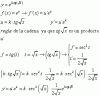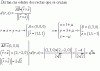-
Dar una ecuacion parametrica de una recta en R3 que: a) es perpendicular al plano π:4x-2y+z=3 y pasa por el punto (0,1,-2).rta .L≡(x,y,z)=λ(4,-2,1)+(0,1,-2). B) es paralela a los planos π1:3x-y+2z=4 y π2:y+z=3 simultañeamente y pasa por el punto (1,3,1). C) es perpendicular a la recta L≡(x,y,z)=λ(0,0,1)+(1,3,-2) y esta incluida en el plano π:x+y+z=2. Preciso el b y el c.
-
Ecuación de una función lineal, que pasa por el punto (1,-1) y por el punto (0,-2)
Alguien me la podría resolver y decirme cual es el proceso. Gracias, es que estoy un poco pérdida con el tema de las funciones.
-
1)Derivada de e^ktg√x
Solución: ke^tg*√x/2√x*cos²√x
2) derivada de cos 1-e²x/1+e²x
3) derivada de la(tgx)²
Me cuesta hacer estas derivadas alguien me las puede desarrollar por favor!!!