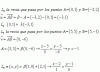-
Hola cómo hago la completacion de cuadrados de esta ecuación 4x²+8x-2?
Tengo que saber hacerlo de la siguiente manera, donde hay que ir sacando el cuadrado del primero y así sucesivamente por ejemplo:
3x²-5x+12=3(x²-5/3x)+12=3[x²+2x(-5/6)+(-5/6)²-(-5/6)²]+12=3[(x-5/6)²-25/6]+12=3(x-5/6)²-25/6+12
-
Dar una ecuacion parametrica de la recta paralela a L:x=2 que pasa por (3,8)


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Dar una ecuacion implicita de la recta perpendicular a L≡(x,y)=λ(2,3)+(1,2) que pasa por (5,-2). Tomo el vector normal (3,-2),lo uso como vector director y queda L1≡(x,y)=β(3,-2)+(5,-2). Ecuacion continua x-5/3=y+2/-2 y la ecuacion implicita es -2x-3y+4=0 es correcto?.desde ya gracias.
-
Dadas L1≡(x,y)=λ(5,-1)+(2,1); L2 la recta que pasa por los puntos (0,1) y (-3,2); L3 la recta que pasa por los puntos (5,5) y (5,-1); L4≡(x,y)=β(1,0)+(2,1) y L5:x+3y=-1 a) dar ecuaciones implicitas para l1,l2,l3 y l4.b) dar una ecuacion parametrica para L5. Quisiera saber si esta Bien,desde ya gracias.