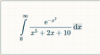-
Hola buenas, tengo una pregunta sobre calculadoras.
Normalmente suelo utilizar este sitio (https://www.symbolab.com/solver/integral-calculator/%5Cint%20cos%5E%7B4%7D%20x%20dx) para comprobar que mis derivadas e integrales son correctas o cuando necesito un poco de inspiración. Sabeis si existe alguna calcudora que esté especializada en derviadas e integrales y que proporcione una funcionalidad similar a la web app que he nombrado? Muchas gracias.
-
-
Buenas, con qué integral debo comparar la siguiente integral impropia (que no tiene primitiva) para de esta manera saber si converge o diverge?
Gracias


Antonio Silvio Palmitano
el 9/1/20Vamos con una orientación.
Observa que el numerador del argumento toma valores positivos el intervalo de integración: [0;+∞)
Observa que el denominador consta de tres términos positivos, que toma valores positivos en el intervalo de integración: [0;+∞), y que su valor mínimo es 10.
Luego, tienes el argumento de tu integral:
f(x) = e-x²/(x5 + 2x + 10) ≤ minimizas el denominador ≤ e-x²/10 = g(x);
luego, aplicas el Criterio de Comparación, y queda:
0∫+∞ f(x)*dx ≤ 0∫+∞ g(x)*dx, sustituyes las expresiones de los argumentos de las integrales, y queda:
0∫+∞ [e-x²/(x5 + 2x + 10)]*dx ≤ 0∫+∞ [e-x²/10]*dx ≤ (1/10)*0∫+∞ e-x²*dx,
y observa que la integral remarcada es convergente (recuerda la gráfica "campana de Gauss), y esto se demuestra por medio de un recurso que apela a una integración doble, por lo que puedes concluir que la integral de tu enunciado:
0∫+∞ [e-x²/(x5 + 2x + 10)]*dx es convergente.
Espero haberte ayudado.
-
Buenas, el criterio de Gauss dice lo siguiente:
Mi pregunta es, como sé si una serie es menor o mayor que otra? Porque puede ser que una serie comience en 1 pero decrezca y otra empiece en 0 pero crezca...
Cómo sé si una es mayor o menor que otra?
Gracias


Antonio Silvio Palmitano
el 9/1/20Ya te hemos mostrado un ejemplo, pero en general una forma de visualizar la aplicación del Criterio de Comparación es esta:
si la serie tiene términos positivos fraccionarios, con sus numeradores positivos y sus denominadores positivos:
- si maximizas el numerador y/o minimizas el denominador del argumento, entonces obtienes una serie mayor que la anterior;
- si minimizas el numerador y/o maximizas el denominador del argumento, entonces obtienes una serie menor que la anterior.
Espero haberte ayudado.
-
Buenas, la pregunta es si la siguiente sucesión es convergente o divergente.Yo creo que es divergente (pero me gustaría comprobarlo).
Σ [3*ln(n)]/[2*n^2]
lo que yo he hecho es comparar con 1/n (divergente). Al hacer el límite cuando n tiende a infinito de la razón de [3*ln(n)]/[2*n^2] entre 1/n nos da infinito, por lo que el "criterio del cociente" nos dice que si el denominador (1/n) es divergente (lo es), el numerador también lo será. De todas maneras me gustaría comprobarlo.
Muchas gracias.

Antonio Silvio Palmitano
el 9/1/20Recuerda la propiedad: "ln(n) ≤ np, con p > 0, a partir de algún número natural n en adelante".
Luego, puedes aplicar el Criterio de Comparación:
∑(n=1,+∞) [3*ln(n)/(2n2)] =
= (3/2)*∑(n=1,+∞) [ln(n)/n2] ≤
aplicas el criterio, para algún n ≥ n0 (elegimos: p = 0,99):
≤ (3/2)*( ∑(n=1,n0-1) [ln(n)/n2] + ∑(n=n0,+∞) [n0,99/n2] ) =
= (3/2)*( ∑(n=1,n0-1) [ln(n)/n2] + (3/2)*∑(n=n0,+∞) [n-1,01],
y observa que la primera suma es finita, y que la segunda suma remarcada es convergente, y esto lo puedes demostrar por medio del Criterio de la Integral (te dejo la tarea).
Espero haberte ayudado.