Pon foto del enunciado original, por favor.

La recta que piden tiene como vector director PQ=Q-P=(-1,0,0)-(1,1,-3)=(-2,-1,3)  y como  pasa por el punto (4,3,-5) quedaría en forma vextorial 

(x,y,z)=(4,3,-5)+λ(-2,-1,3)

Vamos con otra forma para factorizar el polinomio de tu enunciado.

Tienes el polinomio:

P(x) = 9x² + 12x + 4,

luego, observa que puede escribirse en la forma:

P(x) = (3x)² + 2*(3x)*2 + 2²,

por lo que tienes un trinomio cuadrado perfecto, que es el desarrollo de un binomio elevado al cuadrado, cuyo primer término es 3x y su segundo término es 2, por lo que factorizas, y queda:

P(x) = (3x + 2)².

Luego, puedes plantear la condición que cumplen las raíces:

P(x) = 0, sustituyes la expresión factorizada del polinomio, y queda:

(3x + 2)² = 0, extraes raíz cuadrada en ambos miembros (observa que el índice es par), y queda:

|3x + 2| = 0, luego, por anulación de un valor absoluto, tienes la ecuación:

3x + 2 = 0, restas 2 en ambos miembros, y queda:

3x = -2, divides por 3 en ambos miembros, y queda:

x = -2/3,

por lo que tienes que el polinomio tiene una sola raíz que es racional, y cuya multiplicidad es dos pro provenir de un factor cuadrático.

Espero haberte ayudado.

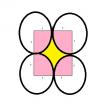
Observa que la figura que es unión de las zonas coloreadas con rosa y amarillo es un cuadrado,

cuya área queda expresada:

A₁ = (2r)² = 4r².

Observa que cada una de las cuatro zonas coloreadas con rosa es un cuarto de círculo cuyo radio es r, 

lo que el área total sombreada con rosa queda expresada:

A₂ = 4*πr²/4 = πr².

Luego, observa que el área de la zona sombreada con amarillo es igual a la resta del área del cuadrado menos el área total de los cuatro cuartos de círculo, por lo que queda expresada:

A = A₁ - A₂, = 4r² - πr² = (4 - π)*r².

Observa que cada uno de los cuatro tramos del borde de la zona sombreada con amarillo es un cuarto de circunferencia, por lo que su perímetro queda expresado:

P = 4*2πr/4 = 2πr.

Espero haberte ayudado.

Observa la figura, en la que hemos extendido hacia el interior a todos los lados de la figura estrela, y en la que hemos trazado las diagonales del hexágono interior.

Observa que la figura estrella quedó dividida en doce triángulos equiláteros, cuyos lados miden: L = 2 cm.

Luego, planteas la expresión del área de uno de los triángulos equiláteros coloreados en función de la longitud de su lado y de la medida de sus ángulos interiores, y queda:

A_T = (1/2)*L²*sen(60°), reemplazas el valor de la longitud del lado, y queda:

A_T = (1/2)*2²*sen(60°), reemplazas el valor exacto del factor trigonométrico, y queda:

A_T = (1/2)*2²*√(3)/2, resuelves, y queda:

A_T = √(3) cm².

Luego, planteas la expresión del área de la figura estrellada (recuerda que está subdividida en doce triángulos equiláteros con medidas iguales), y queda:

A = 12*A_T, reemplazas el valor del área de un triángulo equilátero, y queda:

A = 12*√(3) cm² ≅ 12*1,732 ≅ 20,784 cm².

Espero haberte ayudado.

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Observa que 1 es una raíz del denominador, luego factorizas por medio de la Regla de Ruffini, y tienes que 2 es una raíz doble, por lo que puedes plantear la expresión de tu enunciado en la forma:

(6x² - 19x + 15) / (x-1)(x-2)² = a/(x-1) + b/(x-2) + c/(x-2)² (1),

luego, extraes denominador común en el segundo miembro, y queda:

(6x² - 19x + 15) / (x-1)(x-2)² = ( a(x-2)² + b(x-1)(x-2) + c(x-1) ) / (x-1)(x-2)²,

luego, por igualdad entre expresiones algebraicas fraccionarias con denominadores iguales, tienes que los numeradores también son iguales, por lo que puedes plantear la igualdad entre polinomios:

a(x-2)² + b(x-1)(x-2) + c(x-1) = 6x² - 19x + 15;

luego, como tienes tres coeficientes a determinar, evalúas la igualdad para tres valores distintos (observa que 1 y 2 son dos valores muy convenientes), por ejemplo: 1, 2 y 0, y queda el sistema de ecuaciones:

a + b*0*(-1) + c*0 = 2, y de aquí despejas: a = 2,

c*0 + b*1*0 + c*1 = 1, y de aquí despejas: c = 1,

a*(-2)² + b*(-1)*(-2) + c*(-1) = 15, aquí resuelves coeficientes, y queda:

4a + 2b - c = 15, reemplazas los valores remarcados, y queda:

4*2 + 2b - 1 = 15, resuelves términos numéricos en el primer miembro, y queda:

2b + 7 = 15, y de aquí despejas: b = 4.

Luego, reemplazas los valores remarcados en la igualdad entre expresiones algebraicas señalada (1), y queda:

(6x² - 19x + 15) / (x-1)(x-2)² = 2/(x-1) + 4/(x-2) + 1/(x-2)².

Espero haberte ayudado.

Lo siento pero no podemos ayudaros con dudas de esta asignatura. Espero lo entiendas.

Recuerda la descomposición en factores primos del número natural doce:

12 = 2²*3 (1).

Luego, tienes la expresión de tu enunciado:

(3*w)³) / (12*w)^21/2 = 

distribuyes las potencias en el numerador y en el denominador, y queda:

= 3³*w³ / (12^21/2*w^21/2) = 

reemplazas la expresión señalada (1) en el primer factor del denominador, y queda:

= 3³*w³ / ( (2²*3)^21/2*w^21/2 ) = 

distribuyes la potencia en el primer factor del denominador, y queda:

= 3³*w³ / ( (2²)^21/2*3^21/2*w^21/2 ) = 

aplicas la propiedad de una potencia cuya base es otra potencia en el primer factor del denominador, y queda:

= 3³*w³ / ( 2²¹*3^21/2*w^21/2 ) = 

expresas como multiplicación entre expresiones con potencias con bases iguales, y queda:

= (1/2²¹) * (3³/3^21/2) * (w³/w^21/2) =

aplicas la propiedad de la división entre potencias con bases iguales en los dos últimos factores, y queda:

= (1/2²¹) * (3^3-21/2) * (w^3-21/2) =

resuelves exponentes en los dos últimos factores, y quda:

= (1/2²¹) * (3^-15/2) * (w^-15/2) =

aplicas la propiedad de las potencias con exponentes negativos en los dos últimos factores, y queda:

= (1/2²¹) * (1/3^15/2) * (1/w^15/2) =

resuelves el producto entre los tres factores, y queda:

= 1 / (2²¹*3^15/2*w^15/2).

Espero haberte ayudado.