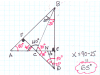
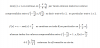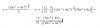-
Buenos días,
No consigo resolver el siguiente problema relacionado con sucesiones. Os dejo lo que he intentado hacer por si alguien podría echarle un ojo y ayudarme a terminarlo.
Un Saludo y Gracias


David
el 29/1/20Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola buenas. Feliz año nuevo a todos los que resuelven dudas por aquí.
Querría saber qué da la integral del seno de Lx, y también qué significa la expresión Lx, si logaritmo neperiano, logaritmo en base 10...
Muchas gracias de antemano.


Antonio Silvio Palmitano
el 2/1/20En general, la expresión: "Lx" o "Lnx" hace referencia al logaritmo neperiano.
Luego, tienes la integral:
I = ∫ sen(Lnx)*dx (*),
planteas el Método de Integración por Partes, y tienes:
u = sen(Lnx), de donde tienes: du = cos(Lnx)*dx/x,
dv = dx, de donde tienes: v = x;
luego, aplicas el método, y queda:
I = x*sen(Lnx) - ∫ cos(Lnx)*dx (1).
Luego, planteas el Método de Integración por Partes para la integral secundaria, y tienes:
u = cos(Lnx), de donde tienes: du = -sen(Lnx)*dx,
dv = dx, de donde tienes: v = x;
luego, aplicas el método, y queda:
∫ cos(Lnx)*dx = x*cos(Lnx) + ∫ sen(Lnx)*dx (2).
Luego, sustituyes los dos términos de la expresión señalada (2) en la ecuación señalada (1), resuelves signos, y queda:
I = x*sen(Lnx) - x*cos(Lnx) - ∫ sen(Lnx)*dx, sustituyes la expresión señalada (*) en el último término (observa que es la integral de tu enunciado), y queda:
I = x*sen(Lnx) - x*cos(Lnx) - I, sumas I en ambos miembros, y queda:
2*I = x*sen(Lnx) - x*cos(Lnx), multiplicas por 1/2 en todos los términos, introduces la constante de integración, y queda:
I = (1/2)*x*sen(Lnx) - (1/2)*x*cos(Lnx) + C,
que es la expresión de la solución general para la integral de tu enunciado.
Espero haberte ayudado.
-
En primer lugar Feliz Año Nuevo para todos.
¿Podrían ayudarme en este problema ?
" Ecuación de la recta paralela a la bisectriz del primer cuadrante que en su intersección con los ejes forma un triángulo de 18 unidades cuadradas de superficie "
Gracias
-
Tengo una duda. ¿Qué método hay para calcular logaritmos? Me refiero a obtener los decimales de un logaritmo, no el valor expresado de forma exacta. Digamos, sé que el log 2 = ln2/ln10
Pero si yo pongo log 2 en una calculadora, me da aproximadamente 0,301 ¿cómo hago para calcularlo manualmente así?


Jose Ramos
el 2/1/20El cálculo del logaritmo manualmente es complicado. De hecho se inventaron para realizar operaciones complejas sin necesidad de recurrir a algoritmos preestablecidos (Hoy, gracias a las calculadoras, han perdido esa funcionalidad, aunque se utilizan en muchos otros ámbitos). Hay métodos numéricos de aproximación para hacerlo. Por ejemplo, supón que quieres calcular el log 2. Sabemos que el log 2 es un valor x, de modo que 10x = 2. Consideramos la función f(x)=10x-2. Se trata de resolver la ecuación 10x-2 = 0. Para resolver estas ecuaciones por métodos numéricos (utilizando reiteraciones) tenemos el método de Newton-Raphson, o el método de la Regula Falsi (en Youtube están explicados) que te permitirían averiguar con un grado de aproximación mayor o menor dependiendo del número de iteraciones, el valor de x, es decir del logaritmo decimal de 2.
Es lo más que se me ocurre.
-
Hola !
Me podría ayudar con esta derivada. Lo tengo que hacer con la tabla de derivadas K (constante ) x f'(x).
Yo la he hecho no se si estará bien, el RESULTADO final está recuadrado en ROJO.
Muchas gracias, por vuestra atención y ayuda.
Le envió la foto:
-
 4ºESO Inecuación. Por favor es correcta la solución que adjunto ejercicio. A la hora de determinar los intervalos correctos para las x me hago bastante lío. No termino de dominarlo. Agradecería cualquier comentario al respecto. Buenas noches.
4ºESO Inecuación. Por favor es correcta la solución que adjunto ejercicio. A la hora de determinar los intervalos correctos para las x me hago bastante lío. No termino de dominarlo. Agradecería cualquier comentario al respecto. Buenas noches.
Clow
el 2/1/20No es correcto. Hallaste los puntos críticos correctamente pero la solución es incorrecta. El signo del numerador te queda positivo/raíz/negativo, el del denominador queda negativo/raíz/positivo, sumas ambos signos, teniendo en cuenta que la raíz del denominador no existe en el signo total y te queda negativo/punto no existencia/positivo/raíz/negativo.
El ejercicio pide menor estricto así que tu solución es:
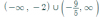
Porque en el intervalo entre -2 y -9/5 el resultado es positivo, así que no va en la solución.


JOSE ANTONIO
el 2/1/20 Hola Clow, muchas gracias por tu mensaje. He comprobado y corregido la solución, (-∞, -2) U (-1.8, ∞), y adjunto de nuevo el ejercicio. No obstante en tu contestación hay cosas que no comprendo y me gustaría saber. ¿Qué quieres decir con el siguiente textos?
Hola Clow, muchas gracias por tu mensaje. He comprobado y corregido la solución, (-∞, -2) U (-1.8, ∞), y adjunto de nuevo el ejercicio. No obstante en tu contestación hay cosas que no comprendo y me gustaría saber. ¿Qué quieres decir con el siguiente textos?“El signo del numerador te queda positivo/raíz/negativo, el del denominador queda negativo/raíz/positivo, sumas ambos signos, teniendo en cuenta que la raíz del denominador no existe en el signo total y te queda negativo/punto no existencia/positivo/raíz/negativo."
-
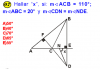
te repregunto por que en la parte final tienes en la ultima linea x +100 esto es en b lo entiendo pero luego repites la x no entiendo por que esa otra x le sumas 40 que debe ser el 40 del vertice c espero me lo explique con un grafiquito si puedes por favor se le agradece