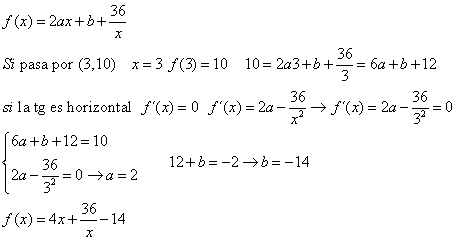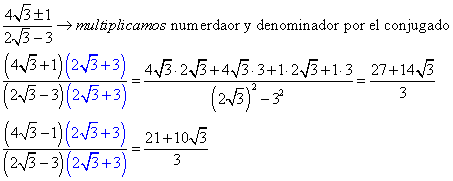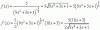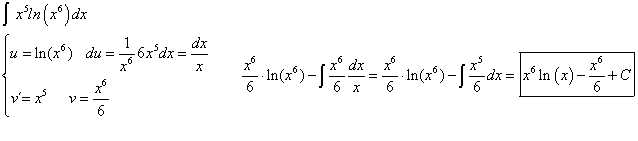-
Adjunto ejercicio realizado. Por favor aclararme un poco que quiere decir el comentario de mi libro que dice literalmente: “El numerador cambia de signo en x = 3, y el denominador en x = -5, por lo que la recta....."


Antonio Silvio Palmitano
el 30/12/19Observa que la expresión del primer miembro de la inecuación que tienes en tu enunciado está definida en el conjunto: R - {-5,3],
pués x1 = -5 el valor para el cuál el denominador toma el valor cero.
Luego, has planteado correctamente que el numerador toma el valor cero para x2 = 3.
Luego, observa que te han quedado definidos tres subintervalos, para los cuáles tomas un valor representante, evalúas la expresión del primer miembro de tu inecuación, y queda:
I1 = (-∞;-5), representado por: x = -6, para el que tienes: (-6-3)/(-6+5) = -9/(-1) = 9 > 0,
I2 = (-5;3), representado por: x = 0, para el que tienes: (0-3)/(0+5) = -3/5 < 0,
I3 = (3;+∞), representado por: x = 4, para el que tienes: (4-3)/(4+5) = 1/9 > 0,
y recuerda que la expresión del primer miembro de la inecuación de tu enunciado toma el valor cero para x2 = 3.
Luego, observa que la expresión mencionada toma valores positivos o iguales a cero en el conjunto solución:
S = I1 ∪ I3 ∪ {3} = (-∞;-5) ∪ (3;+∞) ∪ {3} = (-∞;-5) ∪ [3;+∞).
Espero haberte ayudado.

David
el 30/12/19Hola!
A ver, más directo: lo que quiere decir la frase en negrita es que cuando x=3, x-3 cambia de signo a partir de x=3. un valor más pequeño de 3 va a resultar negativo en ese factor hasta que, una vez llegas a x=3 (3,01, por ej) es positivo. Lo mismo para el factor del denominador.
Espero que ya haya podido responderte y aclararte la duda.
-


Breaking Vlad
el 8/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Antonio Silvio Palmitano
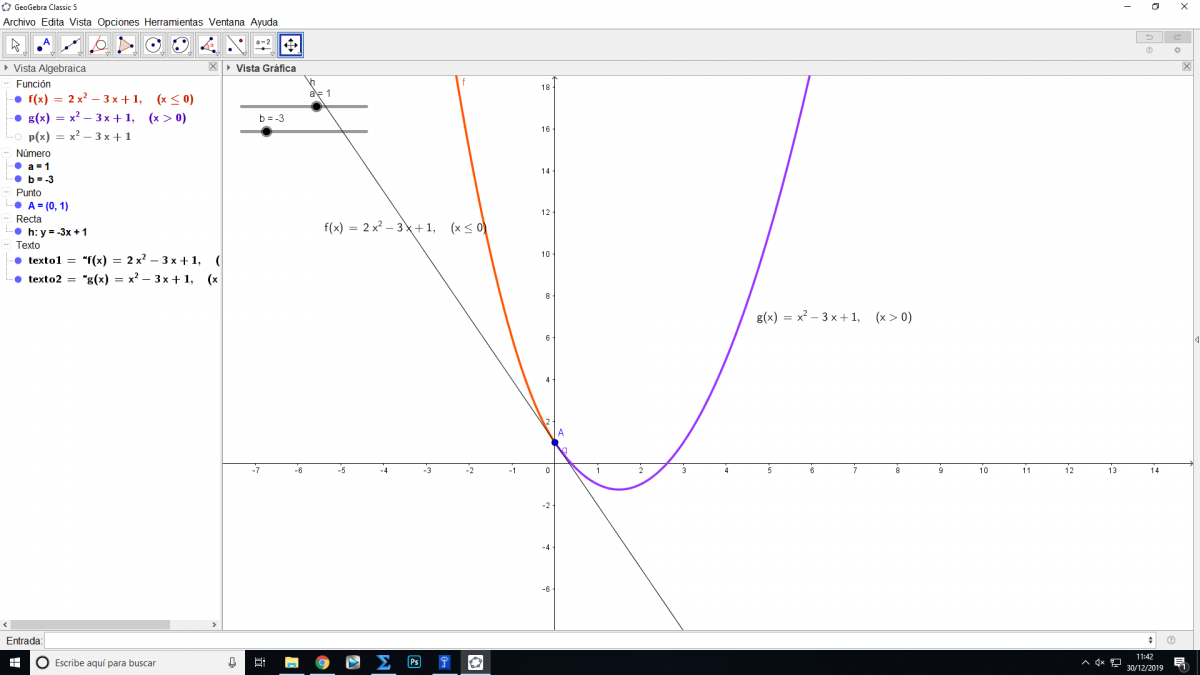
el 30/12/19Tienes la expresión de la función, cuyo dominio es R, en dos trozos, y observa que las expresiones de dichos trozos corresponden a funciones continuas en todos los elementos de sus intervalos de validez, por lo que el valor notable a estudiar es: a = 0.
Luego, planteas la definición de continuidad de la función en a = 0, y queda:
1°)
f(0) = 2*02 - 3*0 + a = a;
2°)
Lím(x→0-) f(x) = Lím(x→0-) (2*x2 - 3*x + a) = a,
Lím(x→0+) f(x) = Lím(x→0+) (x2 + b*x + 1) = 1,
y para que el límite exista, planteas la igualdad de los límites laterales, y queda la condición: a = 1;
3°)
observa que el valor de la función en el valor notable es: f(0) = 1, y que el límite de la función para este valor queda: Lím(x→0+) f(x) = 1,
por lo que tienes que la función es continua si y solo si se cumple: a = 1.
Luego, reemplazas el valor remarcado en la expresión de la función que tienes en tu enunciado, y queda:
f(x) =
2*x2 - 3*x + 1 si x ≤ 0,
x2 + b*x + 1 si x > 0.
Luego, planteas la expresión de la función derivada, y queda:
f'(x) =
4*x - 3 si x < 0,
a determinar si x = 0,
2*x + b si x > 0,
y observa que las expresiones del primer trozo y del tercer trozo corresponden a funciones continuas en todos los elementos de sus intervalos de validez, por lo que el valor notable a estudiar es: a = 0;
luego, puedes plantear los límites laterales para el valor notable, y queda:
Lím(x→0-) f'(x) = Lím(x→0-) (4*x - 3) = -3,
Lím(x→0+) f'(x) = Lím(x→0+) = b,
y para que el límite exista, planteas la igualdad de los límites laterales, y queda la condición: b = -3,
y observa que el valor de la función derivada para el valor notable es: f'(0) = -3,
y observa además que la función derivada es continua en este valor notable;
luego, reemplazas este último valor remarcado en la expresión de la función que ya tienes planteada, y en la expresión de la función derivada, y queda:
f(x) =
2*x2 - 3*x + 1 si x ≤ 0,
x2 - 3*x + 1 si x > 0;
f'(x) =
4*x - 3 si x < 0,
-3 si x = 0,
2*x - 3 si x > 0.
Y observa que también podrías haber planteado la derivabilidad de la función en el valor notable por medio de la definición de función derivada.
Espero haberte ayudado.
-
Hola
Me podría resolver esta derivada, no se como se haría por más vueltas que doy no lo consigo hacer. Sería muy importante que me la resolviera. Muchas gracias.
Lo tengo que resolver por la tabla de derivadas k (constante) x (f'(x))
Ahí le mandó la foto.