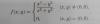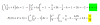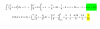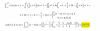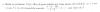-
 Hola unicos ,no me sale este ejercicio, ya el k = es -1/2, P(2,5 ≤ X ≤ 3) entonces desarrollo de 3 seria igual a 1 ya que remplaso k y es 3/2 - 1/2=1 y 2,5 seria 3/4 ya que (5/2 por 1/2) -1/2 es 3/4 ,despues al 1 le resto 3/4 y es 1/4 ,que estoy haciendo mal?,la respuesta es la D
Hola unicos ,no me sale este ejercicio, ya el k = es -1/2, P(2,5 ≤ X ≤ 3) entonces desarrollo de 3 seria igual a 1 ya que remplaso k y es 3/2 - 1/2=1 y 2,5 seria 3/4 ya que (5/2 por 1/2) -1/2 es 3/4 ,despues al 1 le resto 3/4 y es 1/4 ,que estoy haciendo mal?,la respuesta es la D

Jose Ramos
el 27/12/19No se halla sustituyendo en la función de densidad como haces tú, sino que se sustituye en la función de distribución:
Tienes dos formas más de hacerlo:
1ª) Tienes que saber hallar la función de distribución a partir de la función de densidad. (para eso hay que integrar)
2º) Si la función de densidad es una recta, como en este caso, se puede hacer gráficamente calculando el área de un polígono mediante su fórmula.


Antonio Silvio Palmitano
el 27/12/19Planteas la condición que cumple una función de densidad de probabilidad, recuerda que debe tomar valores positivos, y queda:
-∞∫+∞ f(x)*dx = 1, y como tienes que la función toma valores distintos de cero en el intervalo[1,3], tienes que la integral del primer miembro queda:
1∫3 f(x)*dx = 1, sustituyes la expresión general de la función para el intervalo indicado que tienes en tu enunciado, y queda:
1∫3 ([1/2]*x + k)*dx = 1, integras (indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
[ (1/4)*x2 + k*x ] = 1, evalúas, y queda:
( (9/4) + 3*k ) - ( (1/4) + k ) = 1, distribuyes agrupamientos y reduces términos semejantes en el primer miembro, y queda:
2*k + 2 = 1, y de aquí despejas: k = -1/2;
luego, reemplazas este valor remarcado en la expresión de la función de densidad de probabilidad que tienes en tu enunciado, y queda:
f(x) =
(1/2)*x - 1/2 si 1 ≤ x ≤ 3,
0 en cualquier otro caso.
Luego, tienes para la probabilidad de tu enunciado:
p(2,5 ≤ x ≤ 3) =
= 2,5∫3 f(x)*dx = sustituyes la expresión de la función de densidad de probabilidad, y queda:
= 2,5∫3 ( [1/2]*x - 1/2 )*dx = extraes factor común escalar, y queda:
= 2,5∫3 ( [1/2]*[x - 1] )*dx = extraes el factor escalar, y queda:
= (1/2) * 2,5∫3 (x - 1)*dx = integras (indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
= (1/2) * [ (1/2)*x2 - x ] = evalúas, y queda (observa que expresamos a los números en forma fraccionaria):
= (1/2) * ( (9/2 - 3) - (25/8 - 5/2) ) = resuelves agrupamientos en el segundo factor, y queda:
= (1/2) * ( 3/2 - 5/8 ) = resuelves el segundo factor, y queda:
= (1/2) * ( 7/8 ) = resuelves, y queda:
= 7/16,
por lo que puedes concluir que la opción señalada (D) es la respuesta correcta.
Y también tienes otra forma para plantear y resolver el problema:
haces la gráfica de la función densidad de probabilidad para el intervalo de interés: 2,5 ≤ x ≤ 3,
y observa que es un segmento incluido en el primer cuadrante, al que al proyectarlo sobre el eje OX determina un trapecio rectangular,
cuya base menor (segmento vertical de la izquierda) mide: b = 3/4, cuya base mayor (segmento vertical de la derecha) mide: B = 1, y cuya altura (segmento determinado sobre el eje OX) mide: h = 1/2;
luego, puedes plantear que la integral de probabilidad es igual al área del trapecio determinado por la gráfica de la función y el eje OX para el intervalo de interés, por lo que tienes (recuerda la expresión del área de un trapecio):
p(2,5 ≤ x ≤ 3) =
= (1/2)*(B + b)*h = reemplazas los valores remarcados, y queda:
= (1/2)*(3/4 + 1)*(1/2) = resuelves el segundo factor, y queda:
= (1/2)*(7/4)*(1/2) = resuelves, y queda:
= 7/16.
Espero haberte ayudado.
-
Hola Antonio!, gracias por tu respuesta... Agradezco de antemano si puedes aclararme lo siguiente...
Te cuento que no es log3(4-2) (log3 (4 elevado a la menos 2) ... Es log3(4-2) (log de 4 menos 2)
Reescribo lo que me enviastecomo log3(4-2) = (-2)*log3(4)
tenemos que:
log3(4) / log3(4-2) = log3(4) / [(-2)*log3(4)] = ...
simplificando
... = 1 / (-2) = -1/2
por otro lado:
como 9=32 y 1/3=3-1
tenemos que:
log5(9) / log5(1/3) = log5(32) / log5(3-1) = ...
y como log5(32) = 2*log5(3) y log5(3-1) = (-1)*log5(3)
... = 2*log5(3) / [-1*log5(3)] = ...
simplificando
... = 2 / (-1) = -2
Por lo tanto tenemos que:
log3(4) / log3(4-2) = -1/2 y log5(9) / log5(1/3) = -2
por otro lado, tenemos que:
log7/3([(5/9)*x - 1]4) = 4*log7/3([5/9]*x - 1)
Ahora bien, volviendo al principio y sustituyendo tenemos:
-1/2 - 2 = 4*log7/3([5/9]*x - 1)
-5/2 = 4*log7/3([5/9]*x - 1)
-5/8 = log7/3([5/9]*x - 1)
aplicamos la definición de logaritmo:
(7/3)-5/8 = (5/9)*x - 1
(3/7)5/8 = (5/9)*x - 1
(3/7)5/8 + 1 = (5/9)*x
y despejamos la x
x = (9/5)*((3/7)5/8 + 1).
Espero haberte aclarado tus dudas.
-
Hola Unicoos!!!
Si antonio Silvio no puede responder, espero la gentileza de algún otro unicoo... le hablo a Antonio silvio, porque él me respondió diciéndome:Tienes el primer término de la ecuación:
log3(4) / log3(4-2) = aplicas la propiedad del logaritmo de una potencia en el denominador, y queda:
= log3(4) / [-2*log3(4)] = simplificas, y queda: ← En este paso llevas el 2 como producto y el 2 está restando no es exponente del 4 → Es log3(4) / log3(4-2)
= 1 / (-2) = -1/2 (1).
Me puedes ayudar a aplicar la propiedad en log3(4) / log3(4-2)Desde ya muchísimas gracias!!!
Esto es lo que yo había hecho... Según lo que me enviaste no había que aplicar la propiedad de cambio de base...

Antonio
el 27/12/19Lo vamos a hacer por pasos:
como log3(4-2) = (-2)*log3(4)
tenemos que:
log3(4) / log3(4-2) = log3(4) / [(-2)*log3(4)] = ...
simplificando
... = 1 / (-2) = -1/2
Por lo tanto tenemos que: log3(4) / log3(4-2) = -1/2
por otro lado:
como 9=32 y 1/3=3-1
tenemos que:
log5(9) / log5(1/3) = log5(32) / log5(3-1) = ...
y como log5(32) = 2*log5(3) y log5(3-1) = (-1)*log5(3)
... = 2*log5(3) / [-1*log5(3)] = ...
simplificando
... = 2 / (-1) = -2
Por lo tanto tenemos que: log5(9) / log5(1/3) = -2
por otro lado, tenemos que:
log7/3([(5/9)*x - 1]4) = 4*log7/3([5/9]*x - 1)
Ahora bien, volviendo al principio y sustituyendo lo que está en negrita tenemos:
-1/2 - 2 = 4*log7/3([5/9]*x - 1)
-5/2 = 4*log7/3([5/9]*x - 1)
(-5/2)/4 = 4*log7/3([5/9]*x - 1)/4
-5/8 = log7/3([5/9]*x - 1)
aplicamos la definición de logaritmo:
(7/3)-5/8 = (5/9)*x - 1
(3/7)5/8 = (5/9)*x - 1
(3/7)5/8 + 1 = (5/9)*x
y despejamos la x
x = (9/5)*((3/7)5/8 + 1).
Espero haberte aclarado tus dudas.
-
hola, tengo este ejercicio de diferenciabilidad. En la primera parte me pide que la estudie en el punto (0,0), hasta aí bien un ejercicio de diferenciabilidad normal. Mi duda es en la segunda parte del ejercicio en la que me piden que estudie la diferenciabilidad en el punto (1,0). Intenté hacerlo mediante el limite de definicion de diferenciabilidad (tras calcular el gradiente, etc...) y el resultado me da 2cos@. El problema es que en este caso no sé que me debería dar el limite, ni si lo he hecho bien. A lo mejor se podría afirmar que es diferenciable puesto que la funcion es continua en ese punto, existen las derivadas parciales y estas tambien son continuas? Una orientacion porfavor?
Gracias de antemano


Antonio Silvio Palmitano
el 27/12/19Para el punto en estudio: A(1,0), puedes plantear las expresiones de las funciones derivadas parciales (observa que este punto pertenece al sector del dominio de la función donde es válida la primera expresión de la función, y que puedes aplicar la Regla de Derivación para una División de Funciones), y queda:
fx(x,y) = [ 3x2*(x2 + y2) - (x3 - y3)*2x ] / (x2 + y2)2 = (x4 + 3x2y2 - 2xy3) / (x2 + y2)2,
fy(x,y) = [ -3y2*(x2 + y2) - (x3 - y3)*2y ] / (x2 + y2)2 = (-y4 - 3x2y2 - 2x3y) / (x2 + y2)2,
y observa que ambas expresiones son continuas en R - {(0,0)} (observa que tienes dos expresiones que son divisiones entre funciones continuas, y cuyos denominadores no toman el valor cero en el conjunto mencionado),
luego, recuerda el Teorema que seguramente has estudiado en clase:
"si fx(x,y) y fy(x,y) son continuas en un punto A(x0,y0) perteneciente al dominio de la función, entonces f(x,y) es diferenciable en dicho punto",
por lo que tienes que la función es diferenciable en R - {(0,0)} y, por lo tanto, puedes concluir que la función es diferenciable en tu punto en estudio: A(1,0), que es un punto perteneciente a R - {(0,0)}.
Espero haberte ayudado.
-
Problema de la Regla de la Cadena.
Un dron vuela horizontalmente a una altura de 500 m alejándose de un reflector situado en el suelo. El reflector gira proyectando una señal luminosa que ilumina en todo momento al dron conforme se aleja. Si el reflector gira a una velocidad constante de 1/20 rad/s, ¿a qué velocidad avanza el dron en el instante en que el ángulo α es 60º?
Muchas gracias

Antonio
el 27/12/19Calculemos la función que relaciona espacio (m) recorrido por el dron y ángulo (rad) del reflector, para ello usaremos trigonometría:
e(θ)=500 tanθ
por otro lado, calculemos la función que relaciona ángulo (rad) del reflector con el tiempo (seg), considerando t=0 cuando el dron se encuentra sobre la perpendicular del reflector:
θ(t)=t/20
ahora, pasamos los grados a radianes:
θo=60º=π/3 rad
calculamos cuanto tiempo debe pasar para que el dron alcance esa posición:
to=20π/3 seg
ya podemos calcular la velocidad:
v(t)=de/dt=de/dθ · dθ/dt = 500/cos2θ · 1/20
y por último, sustituimos:
v(20π/3)= 500/cos2(π/3) · 1/20 = 100 m/seg
-
Sea X una variable aleatoria con distribución N ~ (18, 3). Conteste verdadero (V) o falso (F) a las siguientes proposiciones
__La probabilidad de que la variable aleatoria tome valores mayores a 30 es cero
La respuesta es Falso ,pero yo lo resolvi Z<(30-18)/3 y me da 4,pero el 4 si no es 0 entonces que numero representaria?,de antemano gracias¡¡