¿Está bien desarrollado? Gracias

Se considera un sistema de unidades en el que la unidad de longitud es el kilómetro, la unidad de masa la tonelada y la unidad de tiempo la hora. ¿Cuántas unidades de fuerza de este sistema corresponden a una unidad de fuerza del SI? ¿Y del CSG? Resolver las mismas cuestiones para las unidades de potencia y de presión.

Hoola! tengo el siguiente ejercicio:

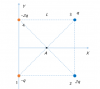
Un electrón parte de la posición indicada en la figura con velocidad inicial v0= 5 . 10^6 m/s formando un ángulo de 45º con el eje X. El campo eléctrico tiene la dirección Y positiva y su módulo es de 3,5 . 10^3 N/C ¿Sobre qué placa y en qué lugar chocará el electrón?

Bueno, yo he planteado esto:

F=qE Si q negativa, la fuerza en contra del campo V0= 5 .10^6 m/s y= y0 + v0. sen α . t -1/2gt^2 F= m.a


Esto está mal:
x=v0.cos α .t lo igualé a la expresión de y pero no sale, está mal. 
Gracias

hola unicoos me pueden ayudar por favor 

una esfera de masa 0.6kg se desplaza con velocidad de 8m/s. en un cierto instante se fragmenta en dos pedazos A y B, tal que el fragmento A se desplaza con velocidad de 12 m/s, en dirección que forma un ángulo de 60º con la dirección inicial. El fragmento B en una dirección ortogonal al del fragmento A, formando en consecuencia, un ángulo de 30º con la dirección inicial. Calcular la masa del fragmento A y la velocidad del fragmento B

Gracias

AYUDA! necesito ayuda con este ejercicio por favor! les agradecería cualquier tipo de guía u.u 

Hola,

quisiera saber donde me equivoco (supongo que el planteamiento esta mal desde el inicio pero estoy bastante pez todavía)

El problema:
Un globo asciende verticalmente en la atmosfera a una velocidad constante de 15m/s y se deja caer de él un saco de arena, que llega al suelo al cabo de 10seg. Prescindiendo del rozamiento del aire, determina a que altura estaba el globo cuando se dejó caer el saco. (Solución y₀=341m)


e=e₀+v₀.t-1/2.g.t²

0=e₀+15x10-0,5x9,81(10)²= 150-490,5=-340.5

Hola,  ¿Resuelvo bien este ejercicio? Gracias

Determinar el campo eléctrico en el punto A de la siguiente figura formado por cuatro cargas colocadas en los vértices de un cuadrado de lado L.

Hola, alguien me podría ayudar con el siguiente problema? Dice así:

Un bloque de masa 35 kg está sujeto por una cuerda que se encuentra enrollada sobre un cilindro horizontal de masa 94 kg y radio 83 mm, que puede girar sobre su eje. Calcular:

a) el módulo de la aceleración lineal del bloque;

b) la tensión de la cuerda cuando se suelta el bloque

Gracias de antemano!

Hola me gustaría que por favor me ayudarais con este problema.

Un satélite artificial de 200 kg gira en una órbita circular a una altura h sobre la superficie terrestre.Sabiendo que a esa altura el valor de la aceleración de la gravedad es la mitad del valor que tiene en la superficie terrestre,averigua:

a)La velocidad del satélite

b)Su energía mecánica.Datos: radio medio de la Tierra 6,37x10^6 m.

Hola por favor me pueden ayudar con esto?? no se que formulas usar!!!

Buen día a todos, tengo un dilema al realizar este problema, no me sale por ningún método que ocupe, el libro da como respuesta 11.6 cm, ni idea de como llegar  ese resultado.

Un resorte de masa despreciable tiene una constante de fuerza k=1600 N/m. El resorte se coloca verticalmente con un extremo en el piso, y se deja caer sobre él un libro de 1.20 kg desde una altura de 0.80 m. Determine la distancia máxima que se comprimirá el resorte.