-
Hoka me ayudan con este ejercicio
1) determinar el trabajo que debe hacer un agente externo para mover una carga q>0 desde el punto A hasta el C.
Discuta significado físico del signo.
El hilo es finito con una distancia L.
Yo pensé sacar el campo eléctrico para el eje y luego calcular el trabajo pero no se si la carga puede de pasar por el hilo??? -
Buenas, tengo una duda sobre el teorema de la energía cinética, para demostrarlo, el incremento de desplazamiento se sustituye por la formula del MRUA, ¿entonces solo se puede utilizar en caso de MRUA?
Gracias^^ -
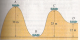
Un coche de montaña rusa, sube hasta el punto A en el cual éste y sus gritones ocupantes, son lanzados pista abajo partiendo del reposo. Suponiendo que no hay fricción, calcule la rapidez en los puntos B, C y D


Francisco Gutiérrez Mora
el 12/7/16Vamos a verlo, Ramiro: Se trata de aplicar conservación de la Energía.
Lo vamos a hacer por tramos:
Tramo AB: EpA=EcB→m·g·h=0.5m·VB²→10·30=0.5V²→VB=√300/0.5=24.49 m/s
Tramo BC: EcB=EpC+EcC→0.5·m·VB²=m·g·h+0.5·m·VC²→0.5·24.49²=10·25+0.5VC²→VC=√(299.88-250)/0.5=9.99 m/s
Tramo CD:EcC+EpC=EcD+EpD→0.5·m·VC²+m·g·hC=0.5·m·VD²+m·g·hD→0.5·9.99²+10·25=0.5VD²+10·12→44.88+250-120=0.5VD²→VD=√174.88/0.5=18.78 m/s
Un Saludo, amigo. -
HELP ME !El mecanismo del rifle de un juguete se compone de un resorte de constante desconocida. Cuando el resorte se comprime 0.12 m, el rifle es capaz de lanzar un proyectil de 35 g hasta una altura máxima de 20 m cuando se dispara verticalmente desde el reposo.
a) Ignore todas las fuerzas resistivas y determine la constante del resorte.
b) Determine la velocidad del proyectil cuando está a una altura de 10 m.


Francisco Gutiérrez Mora
el 12/7/16Vamos a ver: La energía elástica del resorte se convierte en energía potencial en la altura máxima, es decir cuando su velocidad sea cero:
a)Ee=EP→0.5·k·x²=m·g·h→0.5·k·0.12²=0.035·10·20→k=7/7,2·10-³=972.22
b) El trabajo realizado habrá consumido toda la energía:
W=Ee=Ep=7 Julios: como W=F·d→7=20 F→F=7/20=0.35 N
Si tenemos en cuenta que F=m·a→0.5=0.035a→a=14.28 m/s²
Aplicando cinemática tenemos: V²-Vo²=2ax→V√2·a·x=√2·14.28·10=16.90 m/s
Así lo he cocebido. Un Saludo.

Dwilliams
el 12/7/16Para el inciso b) creo que no sería valida la opción dada por Francisco G por varios motivos,la respuesta más logica sería seguir aplicando la ley de conservación de la energía mecánica
Wfnc= 0
∆Em = 0
Emo = Emf
ECo = Epg
½mv²= mgh simplificando las masas y despejando nos queda
v=√2gh = √2*9,8*10
v=√200 = 14,14 m/s
La otra variante usando la 2da ley del mov a mi entender sería así:
∑F= ma donde la fuerza que actúa sobre le cuerpo es la Fg
Fg= ma
Fg=m * (v²- v²o)/2s Despejando y simplificando las masas y teniendo en cuenta que Fg= mg y s=H
2gH= v²- v²o siendo v²o = 0
v=√2gH
Saludos DWilliams
-
Hola muy buenas.
Tengo la presente duda sobre vectores la cual es la siguiente:
Hace ya tiempo que me he tenido la duda sobre "hacia adonde va el vector", me explico:
Si tengo un vector en el primer cuadrante a 60 grados, expresado normalmente su direccion seria 60° (Forma polar) y su rumbo seria (N30°E) pero si en un ejercicio me dice por ejemplo 30° NE desde donde se inicia la medicion del angulo desde el eje "X" o "Y"
Gracias de antemano. -
Hola, podrían ayudarme por favor, este ejercicio es de fluidos, pero no se muy bien como abordarlo,pensé en hacerlo con el principio de Pascal, pero de ser así ambas presiones deberían ser iguales (verdad?) y en este caso me piden la presión manométrica del gas, entonces estoy un poco confundida, ayuda por favor!!
Gracias. -
Hola Unicoos, podrían ayudarme con este ejercicio por favor :D ! ?
1) Un deslizador de 0,3 [kg] se mueve hacia la derecha a 0,8 [m/s] sobre un riel horizontal sin fricción y choca con un deslizador de 0,2 [kg] que se mueve hacia la izquierda a 2,2 [m/s]. Determine la velocidad de cada deslizador si el choque es elástico. ( respuestas V1= -1,6 [m/s] ; V2=1,4 [m/s] )

Francisco Gutiérrez Mora
el 12/7/16Rodrigo, te dejo una respuesta que he visto de un ejercicio muy parecido en Internet. Es pero que te sirva. Es muy laborioso.Mejor respuesta: La cantidad de movimiento del deslizador que va hacia la derecha, antes del choque es:
p(1) = m.v
p(1) = 0.150kg x 0,8 m/s i (i es el versor en eje x)
p(1) = (0,12 kg.m/s) i
La cantidad de movimiento del deslizador que se mueve hacia la izquierda, antes del choque, es:
p(2) = m.v
p(2) = 0,3kg.(-2,2m/s)i
p(2) = -(0,66kg.m/s).i
La suma de estas dos cantidades de movimiento, es la cantidad de movimiento del sistema antes del choque:
P(antes del choque) = p(1) + p(2)
P(a) = (0,12kg.m/s).i -(0,66kg.m/s).i
P(a) = -(0,54kg.m/s).i
Esta cantidad de movimiento es la que se conserva en el choque elástico. De modo que después del choque, la cantidad de movimiento total sigue siendo -(0,54kg.m/s).i
Como el choque es elástico, debemos suponer que los delizadores, de alguna manera "rebotan", pero de modo que la energía cinética también se conserve.
Antes del choque, la energía cinética para los deslizadores es:
Deslizador que va a la derecha:
Ec = 1/2. m.v²
Ec(1) =0,5 .0,15kg.(0,8m/s)²
Ec(1) =0,048 J
Deslizador que va hacia la izquierda.
Ec(2) = 1/2.0,3.(2,2m/s)²
Ec(2) =0,726 J
De modo que la energía cinética total del sistema antes del choque será:
Ec(antes) = 0,048J + 0,726J
Ec(a) = 0,774 J
Las dos cantidades que deben conservarse después del choque son:
Cantidad de movimiento: -(0,54kg.m/s)i
Energía cinética: 0,774J
Después del choque tenemos:
Delizador 1 (el que iba hacia la derecha)
p(1, después del choque) = m.v(1,d)
p(1,d) = 0,15kg. v(1,d)
Deslizador 2:
p(2, después del choque) = m.v(2,d)
p(2,d) = 0,3kg. v(2,d)
Sumamos estas dos cantidades:
p(1d) + p(2d) = 0,15kg.v(1d) + 0,3kg.v(2d)
-0,54kg,m/s.i = 0,15kg.v(1d) + 0,3kg.v(2d)
Podemos simplificar los kg en ambos miembros:
-0,54 m/s.i = 0,15.v(1d) + 0,3.v(2d)
Voy a multiplicar todo por 100
-54m/s.i = 15v(1d) + 30v(2d)
Podemos dividir todo en 15
-3,6m/s.i = v(1d) + 2v(2d) (esta ecuación es más manejable)
Despejamos v(1d)
v(1d) = -3,6m/s.i - 2.v(2d) (Ecuación 1)
Ahora tenemos que trabajar con las energías cinéticas después del choque.
Para el deslizador 1
Ec(1d) = 1/2.m.[v(1d)]²
Ec(1d) = 0,5.0,15kg.v²(1d)
Ec(1d) = 0,075kg.v²(1d)
Para el deslizador 2
Ec(2d) = 1/2.m.[v(2d)]²
Ec(2d) = 0,5.0,3kg.v²(2d)
Ec(2d) = 0,15kg.v²(2d)
Sumamos estas dos energías cinéticas:
Ec(1d) + Ec(2d) = 0,075kg.v²(1d) + 0,15kg.v²(2d)
Por constancia de la energía cinética, el primer miembro debe valer 0,774J
0,774 J = 0,075kg.v²(1d) + 0,15kg.v²(2d)
Expresamos los joules en N.m =(kg.m/s²).m para cancelar los kg:
0,774 kg.(m/s)² = 0,075kg.v²(1d) + 0,15kg.v²(2d)
0,774 (m/s)² = 0,075 v²(1d) + 0,15.v²(2d) (Ecuación 2)
Ahora debemos trabajar con las ecuaciones 1 y 2 para hallar las velocidades después del choque.
Elevamos la ecuación 1 al cuadrado para reemplazar en ecuación 2:
v(1d) = -3,6m/s.i - 2.v(2d)
v²(1d) = 12,96 (m/s)² + 14,4.v(2d).i + 4.v²(2d)
Ahora reemplazamos esto en la ecuación 2:
0,774 (m/s)² = 0,075.[12,96(m/s)² + 14,4.v(2d).i + 4.v²(2d)] + 0,15.v²(2d)
0,774 (m/s)² = 0,972 (m/s)² + 1,08.v(2d).i + 0,3v²(2d) + 0,15v²(2d)
0,774(m/s)² = 0,972(m/s)² + 1,08.v(2d).i + 0,45.v²(2d)
pasamos el 0,074 al primer miembro para igualar a 0:
0 = 0,198 (m/s)² + 1,08.v(2d).i + v²(2d)
Nos queda una ecuación de 2º grado, de donde podemos determinar v(2d), recuerda que el versor i, cuando se eleva al cuadrado da 1:
Los resultados son:
v(2d) = -2,2m/s.i
v(2d) = - 0,2m/s.i
Si tomamos el primer resultado de la ecuación como la velocidad v(2d), obtenemos para v(1d), según ecuación 1:
v(1d) = -3,6m/s.i -2.v(2d)
v(1d) = -3,6m/s.i - 2.(-2,2m/s)
v(1d) = 0,8 m/s.i
Este par de resultados:
V(2d) = -2,2m/s.i
V(1d) = 0,8m/s.i
dan para la cantidad de movimiento y para la energía cinética después del choque, los mismos valores que para antes del choque. Pero el resultado es trivial, nos dice que los deslizadores simplemente se atravesaron como fantasmas conservando cada uno la velocidad que traía. No puede ser este el resultado porque predice una situación física imposible.
La solución es:
v(2d) = -0,2m/s.i
Según ecuación 1, tendremos para v(1d):
v(1d) = -3,6m/s.i - 2.(-0,2m/s)
v(1d) = -3,2 m/s.i
Ambos deslizadores después del choque se mueven hacia la izquierda (lo cual es lógico, pues el de mayor masa y mayor velocidad se movía hacia la izquierda, es como si se lo hubiera llevado por delante al otro). El deslizador 1 "rebota" y cambia su sentido, y el deslizador 2 disminuye su velocidad pero sigue moviéndose hacia la izquierda.
Espero haber sido medianamente clara. Es un problema fácil desde lo conceptual, pero bastante arduo de transcribir en este contexto por las ecuaciones que implican.

Rodrigo Araya D
el 12/7/16Muchas gracias, de verdad era lo que necesitaba...no se me había ocurrido usar la ecuación de segundo grado ya que llegaba hasta la parte de igualar las ecuaciones y buscaba eliminar alguna pero no con la ecuación.
Ahora todos los ejercicios que me faltan son de esta manera. Gracias !!! -
Hola Unicoos, buenas tardes. Queria pedirles un poco de ayuda con magnetismo.
Tengo entendido que el campo magnetico se mide en Tesla
El flujo de campo se mide en Weber
Pero una fuerza debido a un campo magnetico que unidades tiene? Y la magnitud del momento de torsion en una espira de corriente?
El momento ζ= I B A sen φ... De alli yo deduci que I es amper, B es Tesla y el A metros.. pero no se si esta bien y que unidad es. Muchas gracias -


José Miguel
el 13/7/16Hola Tatiana! En este caso, para calcular el nuevo vector R habrá que empezar a operar por orden: lo primero será meterle mano a lo que hay dentro de los corchetes, y dentro de éstos, primero a lo que tenemos entre paréntesis, la resta de los vectores B - C, de lo que nos queda 9j + 5k.
Lo siguiente es multiplicar por ese -3 (de momento dejamos el menos, ya que el resultado será el mismo) a lo de dentro del paréntesis, obteniendo: -3(9j + 5k)= -27j - 15k
Ahora operamos el vector A: (2i + 5j - 4k) - 27j - 15k = 2i - 11j - 19k
Por último multiplicamos ese resultado por 1/2 y nos queda: i - 11j - 9,5K
Espero que te valga. Saludos!



_Thumb.jpg)





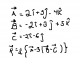




_Thumb.jpg)



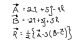

_Thumb.png)
