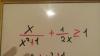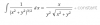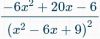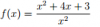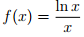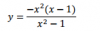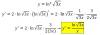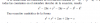-


Antonio Silvio Palmitano
el 14/10/17Tienes la inecuación:
x/(x2+1) + 1/(2x) ≥ 1,
extraes denominador común en el primer miembro, y queda:
(2x2+x2+1) / ( 2x(x2+1) ) ≥ 1,
reduces términos semejantes en el numerador del primer miembro, y queda:
(3x2+1) / ( 2x(x2+1) ) ≥ 1,
haces pasaje de divisores positivos como factores, y queda:
(3x2+1) / x ≥ 2(x2+1),
luego, tienes dos opciones:
a)
si x > 0, haces pasaje de divisor como factor (observa que no cambia la desigualdad), y queda:
3x2+1 ≥ 2x(x2+1), distribuyes en el segundo miembro, y queda:
3x2+1 ≥ 2x3 + 2x, haces pasajes de términos, ordenas términos, y queda:
-2x3 + 3x2 - 2x + 1 ≥ 0, multiplicas en todos los términos de la inecuación por -1 (observa que cambia la desigualdad), y queda:
2x3 - 3x2 + 2x - 1 ≤ 0, observa que 1 es raíz de la expresión polinómica del primer miembro, factorizas por medio de la Regla de Ruffini, y queda:
(x-1)*(2x2-x+1) ≤ 0,
observa que la expresión polinómica del segundo factor no tiene raíces reales, y como su coeficiente principal es positivo, tienes que toma valores estrictamente mayores que cero, luego haces pasaje de factor como divisor (observa que no cambia la desigualdad), y queda:
x - 1 ≤ 0, haces pasaje de término, y queda:
x ≤ 1,
por lo que el intervalo solución queda:
Ia = (0,1];
b)
si x < 0, haces pasaje de divisor como factor (observa que si cambia la desigualdad), y queda:
3x2+1 ≤ 2x(x2+1), distribuyes en el segundo miembro, y queda:
3x2+1 ≤ 2x3 + 2x, haces pasajes de términos, ordenas términos, y queda:
-2x3 + 3x2 - 2x + 1 ≤ 0, multiplicas en todos los términos de la inecuación por -1 (observa que cambia la desigualdad), y queda:
2x3 - 3x2 + 2x - 1 ≥ 0, observa que 1 es raíz de la expresión polinómica del primer miembro, factorizas por medio de la Regla de Ruffini, y queda:
(x-1)*(2x2-x+1) ≥ 0,
observa que la expresión polinómica del segundo factor no tiene raíces reales, y como su coeficiente principal es positivo, tienes que toma valores estrictamente mayores que cero, luego haces pasaje de factor como divisor (observa que no cambia la desigualdad), y queda:
x - 1 ≥ 0, haces pasaje de término, y queda:
x ≥ 1,
por lo que el intervalo solución queda:
Ia = ∅;
luego, planteas la unión de los dos intervalos, y el conjunto solución de la inecuación queda:
S = (0,1].
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 14/10/17Te ayudo con los dos primeros.
1)
Tratamos al numerador (N) y al denominador (D) por separado:
N = -6x2 + 20x - 6 = -2(3x2 - 10x + 3) = -2(x-3)(x-1/3);
D = (x2 - 6x + 9)2 = ( (x-3)2 )2 = (x-3)4;
luego, sustituyes en la expresión del enunciado, y queda:
-2(x-3)(x-1/3) / (x-3)4 = simplificas = -2(x-1/3) / (x-3)3.
2)
Comienza por plantear el límite:
Lím(x→0) f(x) = Lím(x→0) (x2+4x+3)/x2 = ∞ (observa que el numerador tiende a tres y que el denominador tiende a cero),
por lo que tienes que la recta de ecuación: x = 0 es asíntota vertical de la gráfica de la función;
luego, distribuyes el denominador, simplificas, y la expresión de la función queda:
f(x) = 1+ 4/x + 3/x2;
luego, plantea el límite:
Lím(x→∞) f(x) = Lím(x→∞) (1+ 4/x + 3/x2) = 1 (observa que los dos últimos términos tienden a cero),
por lo que tienes que la recta de ecuación y = 1 es asíntota horizontal de la gráfica de la función.
Espero haberte ayudado.
-
El coste de producción de X unidades d'un bien viene dado por la función
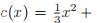
 Sabiendo que el precio de venda de cada unidad es
Sabiendo que el precio de venda de cada unidad es 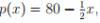 calcula cual es la producción diaria que hace que el beneficio sea maximo.
calcula cual es la producción diaria que hace que el beneficio sea maximo.Parece facil de plantear: b(x) = p(x) - c(x) (-1/3)x2 -35,5x -20 hago la derivada (-2/3)x -35.5 al aillar me sale negativo
-
He aplicado la corrección que me habéis puesto antes pero sigo fallando y no sé en donde.
Me podrían corregir la derivada. Muchas gracias
-