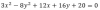logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    Valeria
    el 2/5/17

    De este ejercicio pude hacer solo del ejercicio la parte de g(x), y del que tiene log neperiano solo llegue a realizar la derivada, luego no se como seguir.

    Gracias.

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/5/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Valeria
    el 2/5/17

    Hola Antonio, gracias por la resolucion pero no me queda clara la ultima parte de  los limites en el infinito, si pudieras explicarmela te lo agradezco.


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Victoria Luque Lucena
    el 2/5/17

    Buenos días me gustaría que me ayudarías con este ejercicio, gracias.

    De un tronco de radio r se corta una cuña formada por dos planos que se encuentran en el diámetro del tronco. Uno de los planos es horizontal y el otro forma un ángulo θ con la base. Calcula el volumen de la cuña.

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 2/5/17

    Puedes  considerar una superficie cilíndrica circular de radio r y eje z, cuya ecuación cartesiana es: x2 + y2 = r2.

    Puedes considerar el plano OXY, cuya ecuación es: z = 0, como el plano de la base.

    Luego, puedes considerar un plano "inclinado" como extensión en la dirección del eje OX de la recta del plano OYZ cuya ecuación es ecuación: z = tanθ*y + r*tanθ (observa que el punto de coordenadas A(0,-r,0) pertenece a este plano, al plano anterior y al cilindro)..

    A esta altura de las cosas, es muy conveniente que hagas un gráfico para visualizar mejor la situación.

    Luego, tienes el intervalo de integración para la variable z:

    0 ≤ z ≤ tanθ*y + r*tanθ,

    por lo que puedes comenzar a integrar:

    V = ∫∫∫ 1*dz*dx*cy = ∫∫ [ z ]*dx*dy, para evaluar z entre sus límites de integración con la Regla de Barrow,

    evaluamos y queda:

    V = ∫∫ (tanθ*y + r*tanθ - 0)*dx*dy = ∫∫ (tanθ*y + r*tanθ)*dx*dy (1).

    Luego planteamos el cambio a coordenadas polares (observa que las designamos u y v para no confundir con los datos del enunciado.:

    x = u*cosv

    y = u*senv,,

    con el factor de compensación (Jacobiano): |J| = u,

    y el recinto de integración (observa que es un disco circular completo de radio r):

    0 ≤ u ≤ r

    0 ≤ v ≤ 2π,

    y la integral señalada (1) queda:

    V = ∫∫ (tanθ*u*senv + r*tanθ)*u*du*dv = ∫∫ (tanθ*u2*senv + r*tanθ*u)*du*dv = y puedes continuar la tarea.

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Guillem De La Calle Vicente
    el 2/5/17


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/5/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Lorena Llanos
    el 2/5/17

    Buen día, por favor su ayuda para pasar esta ecuación de hipérbola de su forma general a forma canónica. 


    Mil gracias.

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 2/5/17

    Puedes comenzar por ordenar términos y hacer un pasaje de término y la ecuación queda:

    3x2 + 12x - 8y2 + 16y = - 20,

    luego extraes factor común por grupos:

    3(x2 + 4x) - 8(y2 - 2y) = - 20,

    luego sumas y restas 4 en el primer agrupamiento, sumas y restas 1 en el segundo agrupamiento, a fin de completar trinomios cuadrados perfectos y queda:

    3(x2 + 4x + 4 - 4) - 8(y2 - 2y + 1 - 1) = - 20,

    factorizas los trinomios cuadrados perfectos y queda:

    3( (x + 2)2 - 4 ) - 8( (y - 1)2 - 1 ) = - 20,

    distribuyes y queda:

    3(x + 2)2 - 12 - 8(y - 1)2 + 8 = - 20,

    haces pasajes de términos y queda:

    3(x + 2)2 - 8(y - 1)2 = - 16,

    divides en todos los términos de la ecuación por - 16 y queda:

    - (3/16)(x + 2)2 + (y - 1)2/2 = 1,

    expresas el coeficiente del primer término como divisor ( observa que 3/16 = 1/(16/3) ) y queda:

    - (x + 2)2/(16/3) + (y - 1)2/2 = 1,

    que es la ecuación canónica de una hipérbola con centro de simetría C(-2,1) y eje focal paralelo al eje OY.

    Haz el intento de terminar la tarea, y si te resulta necesario, no dudes en volver a consultar.

    Espero haberte ayudado.




    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Lola
    el 2/5/17




    Hola,el ejercicio dice sabemos que f´(x)=2x f(x) y que f(1)=3 ¿Cuanto vale f´(1)? El tema es de ecuaciones diferenciales!

    Subo la foto de lo que hice,pero no logro entender en donde tengo que remplazar el  f(1)=3 y el  f´(1)


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/5/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Lola
    el 2/5/17

    Hola unicoos, me ayudan con esta ecuacion diferencial? Nose como empezar a despejarla,ya mire los videos pero sigo sin entender 

    (x∧2  -1)y∧2=x.y´

    reply•thumb_up•0 voto/s•flag
    icon

    Axel Morales Piñón.
    el 2/5/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Axel Morales Piñón.
    el 2/5/17

    Supongo que ya sabes integrar y derivar a la perfección para entrar a EDO. Por ello no prolongué la integración.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Joaquín
    el 2/5/17

    Alguien me ayuda? Es que no se como razonarlo

    gracias unicoos


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/5/17

    Sustituye x=0.

    Te va a quedar k-2=0

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Gabriel
    el 2/5/17

    Buenas noches.Necesito ayuda con este limite.No puedo resolverlo.Ya probe con las equivalencias trigonometricas y todo eso, pero sigo sin llegar al resultado. Tengo que usar propiedades.

    Lim(x,y)----(0,0)  Sen^2(x).Sen^2(y)/2xy.tgx.tgy           

    seria, seno al cuadrado de x por seno cuadrado de y todo sobre 2xy por tgx por tgy.

    Gracias de antemano

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/5/17


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Majo Artur ????
    el 2/5/17

    Hola unicoos por favor me pueden ayudar con este ejercicio?

    como lo puedo resolver es que no le entiendo :( 

    mil gracias 


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/5/17

    Revisa operaciones:


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
  • icon

    Zanubia Nufuri
    el 2/5/17

    Hola Unicoos!! sigo teniendo problemas para resolver la derivada y hallar el punto de tangencia. Les agradecere lo puedan resolver...


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/5/17

    tan 45º=1

    Entonces, la pendiente es=1

    Deriva la función:

    Iguala la derivada a 1 y resuelve la ecuación correspondiente.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    suficiente