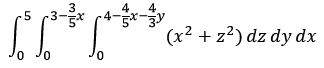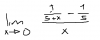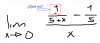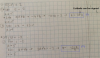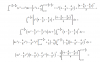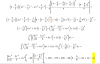logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    Trollcence Lopez
    el 13/4/17

    Buenas tardes como puedo resolver el siguiente ejercicio relacionado con funciones trigonométricas.

    * Sen^-1 (√2/2)

    - Buenas me podéis explicar este ejercicio por favor se que tiene que dar como respuesta R// π/4

    - Pero explicarme por favor, ya vi los videos de unicoos y sigo sin entenderlo (mas precisamente los relacionados con una tabla para los angulos 30 - 60 - 90).

    reply•thumb_up•0 voto/s•flag
    icon

    Javier Marquez
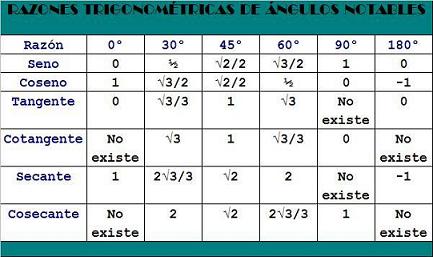
    el 13/4/17

    Hola, primero ten en cuenta que π/4 = 45°  (2π=360°)

    Una forma de hacerlo seria poner en la calculadora sen^-1 (√2/2) y dependiendo si la tienes configurada en radianes o grados sexagesimales te va a dar π/4 o 45 grados

    La otra forma seria viendo esa tabla que dices, tienes que hacer el razonamiento al reves, osea, debes preguntarte para que valor del angulo el seno me da √2/2, y veras que efectivamente corresponde al angulo  π/4 = 45°

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
    icon

    Eusebio Negrut Pardo
    el 13/4/17

    Si coloco en la calculadora sin^-1(√2/2) = 90 y no da 45 grados .-. , estoy haciendo algo mal?


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    nada
    icon

    Javier Marquez
    el 13/4/17

    Sí :/

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Javier Marquez
    el 13/4/17

    Ademas si analisas graficamente la funcion seno veras que no tiene sentido que sin^-1(√2/2) = 90  ya que sin90 = 1

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Eusebio Negrut Pardo
    el 13/4/17

    Cierto si hago la conversión y todo obtengo 45º, pero el ejercicio solo me dan el sen^-1(√2/2) ¿que debo de hacer para obtener los 45º ò π/4?.


    *Tengo que memorizar esta tabla para poder responder correctamente .-.???


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    poco
    icon

    Javier Marquez
    el 13/4/17

    Realmente la tabla solo sirve si los profes no te dejan ocupar calculadora xD, sinceramente no sé porque no te da, acabo de probar con 3 calculadorasa distintas y me da lo mismo, debes tener ojo con los parentesis.

    PD: recuerda que la cosecante es la inversa multiplicativa  del seno mientras que arcoseno ( sen^-1) es la función inversa del seno. 


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Facu Imfeld
    el 13/4/17

    Estimado Eusebio, ¿configuraste tu calculadora en modo Radián?, acabo de hacer arcoseno de tu expresión en mi Casio y me dió pi/4. O sea 45°

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    carlos
    el 13/4/17

    Como resolveria eso

    reply•thumb_up•0 voto/s•flag
    icon

    Ángel
    el 13/4/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Antonio Silvio Palmitano
    el 13/4/17

    Observa que tanto el numerador (N) como el denominador (D) tienden a cero, por lo que el límite es indeterminado.

    Luego, observa el numerador:

    N = 1/(5+x) - 1/5 = extraes denominador común:

    = ( 5 - (5+x) ) / 5(5 + x) = distribuyes el agrupamiento en el numerador:

    = (5 - 5 - x) / x(5 + x) = cancelas términos opuestos en el numerador:

    = (- x) / x(5 + x) = simplificamos = - 1/(5 + x).

    Luego, planteamos el argumento completo:

    N/D = (- 1)/(5 + x) / x = resolvemos = (- 1) / x(5 - x).

    Luego, planteamos el límite

    L = Lím(x→0) (- 1) / x(5 - x) = ∞, ya que el numerador es igual a - 1, y el denominador tiende a cero.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Valentina Villegas Picazo
    el 12/4/17

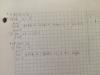
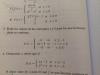    Buenas tardes Unicoos será que me puede no indicar que puedo hacer para resolver el #3? Llegue hasta aquí pero no sabría que más hacer.

    gracias ! 

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio
    el 12/4/17

    Tienes dos ecuaciones con dos incógnitas, resuelve el sistema y listo

    -a + b = 2

    3a + b = -2

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Ángel
    el 13/4/17


    La condición para que la función sea contínua es que los límites laterales coincidan. Has resuelto casi correctamente (excepto un signo) esta condición de igualdad y tienes que resolver el sistema compuesto por (*) y (**), en este caso la solución es por sustitución:


    Sustituyes (*) en (**) y queda:     a= [-2-(2+a)]/3  ------->    (3a)/3=[-2-(2+a)]/3 ----------->     3a=-2-(2+a) ----------->     3a=-2-2-a --------->   4a=-4 ---->    a=-1

    Sustituyes a=-1 en (*) y queda: b=2+(-1) ----->   b=1


    Para que f(x) sea contínua los valores de las constantes han de ser a=-1 y b=1

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    jaime
    el 12/4/17

    ¿hola, hay en la pagina ejercicios resueltos de matemáticas de 3ESO?

    reply•thumb_up•0 voto/s•flag
    icon

    Ángel
    el 12/4/17

    Un montón en los vídeos.... http://www.unicoos.com/cursos/3-eso/matematicas

    y quizá te interese alguno de por aquí... http://www.unicoos.com/cursos/2-eso/matematicas   y   http://www.unicoos.com/cursos/4-eso/matematicas

    si te refieres en formato PDF y eres Pro, David te indicará mejor que yo.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Marcos
    el 12/4/17

    Hola quería saber si me pueden resolver este problema que no se como se hace y lo necesito ya gracias, tengo que hallarlo mediante sistema de ecuaciones pero solo necesito el SISTEMA no la solución


    2: Halla dos números sabiendo que el primero es 12 unidades mayor que el segundo; pero que, si restásemos 3 unidades a cada uno de ellos, el primero sería el doble que el segundo 


    reply•thumb_up•0 voto/s•flag
    icon

    Ángel
    el 12/4/17

    sabiendo que el primero es 12 unidades mayor que el segundo --------->      x=y+12   (*)

    si restásemos 3 unidades a cada uno de ellos, el primero sería el doble que el segundo------------>    x-3=2(y-3)   (**)


    Sustituyendo (*) en (**) obtenemos:

    (y+12)-3=2y-6

    Resolvemos:

    y+12-3=2y-6

    y=15


    Sustituimos y=15 en (*) y obtenemos:  x=15+12=27

    thumb_up•2 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Marcos
    el 12/4/17

    muchas gracias amigo  ;)

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Antonio Silvio Palmitano
    el 12/4/17

    Llamemos x al primer número, y llamemos y al segundo número.

    Luego tenemos:

    x = y + 12 (1) ("el primero es doce unidades mayor que el segundo")

    x - 3 = 2*(y - 3) ("si restamos tres unidades a cada uno, el primero es igual al doble del segundo").

    Luego, tienes x despejado en la primera ecuación, por lo que sustituyes en la segunda y queda:

    y + 12 - 3 = 2*(y - 3), reducimos términos semejantes en el primer miembro, distribuimos el segundo y queda:

    y + 9 = 2*y - 6, hacemos pasajes de términos, reducimos términos semejantes, y queda:

    - y = - 15, multiplicamos por -1 en ambos miembros y queda:

    y = 15, luego reemplazamos en la ecuación señalada (1), y queda:

    x = 15 + 12 = 27.

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Eileen verdugo roca
    el 12/4/17

    hola necesito ayuda urgente ...

    (a+3)(a-3)=      mi consulta es???esto corresponde a un binomio 

    porfavor se lo agradeceria 

    reply•thumb_up•0 voto/s•flag
    icon

    Ángel
    el 12/4/17

    Suma por diferencia = Diferencia de cuadrados

             (a+3)*(a-3)        =           (a2-32)= a2-9  <--------Binomio al cuadrado

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Guillem De La Calle Vicente
    el 12/4/17
    flag

    Demuestre que f(x)=(x)/(x+1) es la solución única a una ecuación funcional.

    Se nos da una función f: ℚ⁺ → ℚ⁺ tal que

    f(x)+f(1/x)=1

    y

    f(2x)=2f(f(x))

    Hallar, con prueba, una expresión explícita para f(x) para todos los números racionales positivos x.

    Cada número que he evaluado es de la forma f(x)=(x)/(x+1) y esto se ajusta claramente a las ecuaciones funcionales, pero no puedo probar que es la única solución. ¿Alguien puede ayudarme? He puesto el comienzo de mi trabajo que me llevó a la conjetura de f(x)=(x)/(x+1).

    Conectando x = 1 damos claramente f (1) = 1/2 y f (2) = 2f (f (1)) = 2f (1/2) que podemos conectar en la primera ecuación para obtener que f (2 ) = 2/3. Trabajando en esta línea he podido demostrar que f (x) = (x) / (x + 1) para valores particulares de x, pero no en general.

    La parte más difícil parece probarla para los enteros pares. Para demostrar x = 8, tenemos f (12) = 2f (6/7) = 4f (3/10) = 4-8f (5/8) = 8f (8/5) -4 = 16f (4/9 ) -4 = 32f (2/11) -4 = 64f (1/12) -4 = 60-64f (12) dándonos f (12) = 12/13. Este será probablemente el principal área de dificultad en la prueba.

    reply•thumb_up•1 voto/s•flag
    icon

    David
    el 17/4/17

    Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

    Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Josue Mosh
    el 12/4/17
    flag

    Hola a todos, tendré examen la próxima semana con integrales de este estilo. ¿Conocen alguna manera óptima para hacerla sin perder tanto tiempo en
    demasiadas operaciones? (Su respuesta es 41).


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 12/4/17


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Josue Mosh
    el 12/4/17

    ¡Te agradezco mucho!

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Epier
    el 12/4/17
    flag

    Hola, me gustaría saber la simplificación de esta función


    Un saludo

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 12/4/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Epier
    el 13/4/17

    y si la respuesta es 'a +'b'c o ninguna cual es?

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?