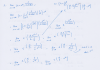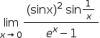-
Hola no se como resolver este ejercicio:
Desde que altura ha caído un objeto sabiendo que llega al suelo con una velocidad de 12m/s?
Cuanto tiempo ha durado la caída?
Estoy en 4 eso

Ángel
el 2/11/16Es un movimiento rectilíneo uniformemente acelerado (MRUA)
Supongo que el objeto parte desde el reposo (Vinicial= 0 m/s), ya que no lo especificas...
Las ecuaciones del MRUA son:
aceleración=a=cte= - 9,8 m/seg2 =gravedad en la tierra (negativa por que el objeto cae, y va en sentido negativo en el eje de coordenadas)
velocidad=velocidad inicial +/- (aceleración*tiempo)
posición=posición inicial +/- (1/2*a*t2)
*Sustituyendo en la ecuación de la velocidad obtendremos el tiempo que duró la caída: 12= 0+9,8*t --> t=12/9,8 --> t= 1,22 segundos ha durado la caída
*Sustituyendo en la ecuación de la posición obtendremos la posición inicial o altura desde que cayó el objeto (como cayó, su posición es 0 metros, el suelo en nuestro sistema de coordenadas...y el tiempo ya lo hemos hallado)
0=posición inicial - (1/2*9,8*1,222 ) --->Posición inicial= (1/2*9,8*1,222 ) ----> Posición inicial= desde 7,35 metros se dejó caer el objeto
P.D: Este tipo de dudas a partir de ahora escríbelas en http://www.unicoos.com/foro/fisica
-
Muy buenas tardes a todos, me gustaría que me ayudasen en una duda que tengo. He tratado de realizar éste límite por la forma de (1 + 1/f)^f = e, pero no me sale, en cambio, si lo hago por L'Höpital si que me da el resultado correcto, que es α/3.
Muchas gracias.
-
Hola
No se como hacer este ejercicio
Y este es similar pero no entiendo a que se refiere con expresion de T


Antonio Silvio Palmitano
el 2/11/16Vamos con una orientación para el ejercicio 1.
Observa bien las expresión de las aplicación T, que consiste en un producto escalar, por lo tanto, los vectores u deben tener tres componentes, por lo que planteamos: u = <x,y,z>, con x, y, z números reales, por lo que tenemos que el dominio es R³.
Luego, observa que el resultado del producto escalar es un número real, por lo que tenemos que el codominio es R.
Luego, vamos con la expresión para esta aplicación:
T(x,y,z) = <x,y,z> • <3,4,5> = 3x + 4y + 5z,
luego puedes demostrar que T es una transformación lineal, como seguramente has hecho en clase con otras aplicaciones.
Para la transformación S, tenemos que el dominio es también R³ y, como su expresión es un producto vectorial, tenemos que su resultado en un vector de tres componentes, por lo que tenemos que el codominio es R³.
Luego vamos con la expresión de la aplicación:
S(x,y,z) = <x,y,z> x <3,4,5> = < 5y-4z , -5x+3z , 4x-3y >,
luego puedes demostrar que T es una transformación lineal, como seguramente has hecho en clase con otras aplicaciones.
-


Antonio Silvio Palmitano
el 2/11/16Va una orientación.
Observa que puedes expresar al argumento del límite como un producto de expresiones:
(senx)²/(e^x - 1) * sen(1/x)
observa que el segundo factor es la expresión de una función acotado entre -1 y 1, y que podemos resolver el límite del primer factor aplicando la Regla de L'Hôpital:
Lím(x-->0) (senx)²/(e^x - 1) = aplicamos LH = Lím(x-->0) 2senxcosx/e^x = 0/1 = 0,
luego, el límite del producto entre una función cuyo límite es 0 por una función acotada, es igual a 0.
Espero haberte ayudado.
-
Cómo puedo representar la función f(x)= e^x * Ln(x)?


David
el 3/11/16Te sugiero estos dos vídeos...
Estudio completo de una funcion exponencialEstudio completo de una funcion logaritmica
Nos cuentas ¿ok? -


David
el 3/11/16El perimetro del rectangulo grande es 2a+2b =66, de donde a+b=33.... b=33-a
La base del rectangulo pequeño sera (b-8) y la altura (a-8). Como el area de ese rectanghulo es 72m² puedes expresar (b-8)(a-8)=72...
Resuelve el sistema de ecuaciones y habrás resuelto casi tu ejercicio...
Pista: Sustituye b=33-a en la 2º ecuacion.... (33-a-8)(a-8)=72.... (25-a)(a-8)=72... 25a-200-a²+8a=72.... -


David
el 2/11/16Para el 4), si existe algun pùnto de corte entre f(x)=(1+x)/e^x e y=x, debe cumplirse que (1+x)/e^x = x... de donde (1+x)/e^x - x = 0
Y ahora aplica Teorema de BOLZANO
Para demostrar que tiene una unica solucion... Teorema de Bolzano-Rolle unica raiz de una funcion
Para el 3), la pendiente se obtiene derivando f(x). Será [e^x - e^x.(1+x)] / (e^x)² = (e^x-e^x-x.e^x)/ (e^x)² = -x.e^x/ (e^x)² = -x/ e^x, que podríamos llamar m(x), expresion que relaciona el valor de x con la pendiente de f(x)... Te sugiero.. Derivada de una multiplicacion y una division 01
Como te piden saber cuando m(x) será minima, tendrás que obtener el minimo de la funcion m(x).
Y para ello, como siempre... Deriva m(x), iguala a 0... Crecimiento y curvatura de una función polinomica -


David
el 2/11/16Si el numero es multiplo de 3, la suma de todas sus cifras (4+2+1+9+x=16+x debe ser multiplo de 3)
Eso nos da diferentes opciones, a saber, x=2, pues 16+2=18 , multiplo de 3.... El numero en este caso sería 421290.
Tambien x=5, pues 16+5=21, tambien multiplo de 3. El numero en este caso sería 421590. (ESA ES LA SOLUCION)....
Ta,mbien x=8, pues 16+8=24, tambien multiplo de 3... El numero en este caso sería 421890.
Comprueba si esos numeros son multiplos de 13, dividiendo entre 13. El resto debe darte 0... O incluso mira el 2º vídeo que te recomiendo más adelante...
Te sugiero.. Criterios de divisibilidad 01 -
Cómo sería la simplificación de cos^3(x ) a través de la fórmula de Moivre?


Antonio Silvio Palmitano
el 2/11/16Puedes plantear la identidad de De Moivre para el cubo de un número complejo genérico con módulo 1 y argumento x:
( cosx + isenx )³ = cos3x + isen3x, luego desarrollamos a la izquierda y queda (resolvemos las potencias de i en cada término):
cos³x + i3cos²x*senx - 3cosx*sen²x - isen³x = cos3x + isen3x, agrupamos términos reales e imaginarios a la izquierda:
( cos³x - 3cosx*sen²x ) + i( 3cos²x*senx - sen³x ) = cos3x + isen3x, luego comparamos términos y tenemos dos identidades:
1) cos³x - 3cosx*sen²x = cos3x (observa que puedes sustituir con la identidad: 1 - cos²x = sen³x, y queda la expresión en función de cosx);
2) 3cos²x*senx - sen³x = sen3x (observa que puedes sustituir con la identidad: 1 - sen³x = cos²x, y queda la expresión en función de senx).
Espero haberte ayudado.