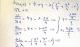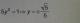-
Hola buenas, soy nuevo aquí. Me estoy preparando para la carrera de matemáticas que empiezo este mes. Resulta que provengo del bachillerato de Ciencias Sociales, por lo que he estudiado este verano integrales, derivadas y matrices mas complicadas. Pero tengo algunas dudas:
-¿ Qué es un modulo de un vector y vector proyección( definición, no formula)
-¿Se podría usar Cramer para sistemas no cuadrados(en el libro sale, pero no es muy explicativo)?
Si surgen más vuelvo a preguntar. Gracias de antemano. ¡La página esta maravillosa, me ha ayudado un montón!
Usuario eliminado
el 1/9/16Hola buenas, sólo te puedo responder a una, el módulo de un vector es la raíz de la suma de las dos componentes al cuadrado, es decir un vector v=(a,b) su módulo es |v|=√(a²+b²) si lo que quieres es una definición técnica busca mejor en internet porque no soy muy de memorieta.
PD:Suerte en la carrera.
-
Usuario eliminado
el 1/9/16Daniel, lambda al hacer propiedad distributiva con el polinomio se queda separado en varias sumas y restas, todas ellas como derivada parcial son constantes excepto la de en medio que multiplica a la y, la derivada una constante k por la variable de grado uno es la constante k:
(kx)'=k, en este ejemplo se deriva obviamente con respecto a x.
-
Este tipo de operación se resuelve en caso de no tener la misma base factorizar(igualar bases) entonces, operar, verdad?( no es este el caso claro)
Pero con las raices cuadradas que se hace se suman?(en caso de multiplicación)
gracias

Antonio Silvio Palmitano
el 1/9/16Observa el numerador (N), puedes distribuir la raíz cuadrada, operar y quedan tres factores:
(6V)(2) * V(2) * (4V)(2) = observa que el mínimo común índice es 12 entre las raíces de índice 6, 2 y 4
= (12V)(2^2) * (12V)(2^6) * (12V)(2^3) = asociamos y queda:
= (12V)(2^11).
Luego expresamos al denominador (D) con raíz de índice 12 y queda:
D = (12V)(2^3).
Luego, expresamos el cociente con índice 12, simplificamos en el argumento y queda:
N/D = (12V)( 2^11 / 2^3 ) = (12V)(2^8) = observa que el índice y el exponente son simplificables por 4
= (3V)(2^2).
Pro lo tanto el resultado final es raíz cúbica de 4.
Recuerda que cuando tienes "una raíz cuyo argumento es otra raíz" debes multiplicar los exponentes, y recuerda también el procedimiento para reducir factores a raíces con índice mínimo común
Espero haberte ayudado. -
Hola¡
esta bien esta derivada parcial? me explican por favor los pasos como la simplifico ahora?
Gracias!

Antonio Silvio Palmitano
el 1/9/16Debes corregir.
Observa que estás derivando con respecto a x (por lo tanto: (y^2) ' = 0), por lo que la expresión queda:
dL/dx = ( 2x*y^2 - (x^2 + 75)*0 ) / y^4 + L
cancelamos el término nulo en el numerador de primer término y queda:
dL/dx = 2x*y^2 / y^4 + L
simplificamos en el primer término y queda:
dL/dx 2x/y^2 + L.
Espero haberte ayudado. -
Hola, me podrian ayudar y decirme en que me he perdido. no me salen todas las soluciones del sistema de ecuaciones, no se ordenarlas en su resolucion para construir 4 soluciones...
El mio es el de boli azul....












_Thumb.jpg)




_Thumb.jpg)