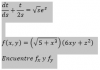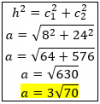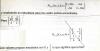-
Esperanza Macarena Diana Liroa
el 2/9/16Hola, a ver si me podéis ayudar con un ejercicio que tengo pendiente casi desde el principio del curso pasado, se lo pregunté a mi profesora, pero no me enteré de nada, la verdad. Se suponía que los ejercicios propuestos eran de inecuaciones, pero uno de ellos era este: |x|=x+5, ¿alguien me podría explicar cómo lo resuelvo?, muchas gracias.
César
el 2/9/16
Jordi García
el 2/9/16Hola Esperanza Macarena Diana Liroa.
Antes de empezar voy a aclararte el siguiente concepto: cuando una variable (x,y...) o un número (-1,0,1...) está entre estos signos | | significa que se coge su valor absoluto, es decir, se coge el número natural. Por ejemplo:
|-5| = 5
|5| = 5
|0| = 0
Ahora, para entender lo que voy a hacer a continuación, mira la explicación en esta página web: http://matematicatuya.com/DESIGUALDADES/S8_Ecuaciones_Absoluto.html
|x| = x + 5 → x = x + 5 → x - x = 5 → 0 = 5 → ∅
|x| = x + 5 → x = -(x + 5) → x + x = -5 → 2x = -5 → x = -2,5
Finalmente vamos a comprobar la solución:
|x| = x + 5 → |-2,5| = -2,5 + 5 → 2,5 = 2,5
¡Un saludo!
-
Marco
el 2/9/16Nelson, no se carga la imagen
Jordi García
el 2/9/16Hola Marco.
En la pregunta que has enviado de esos dos ejercicios sí que se ven las imágenes.
Yo te planteo las posibles causas de por qué no se carga la imagen:
1) La imagen aparece debajo del texto que escribes y cómo gran parte de ésta es blanca, no ves el contenido importante de la imagen porque no bajas hacia abajo, es decir, el fondo blanco de la imagen se camufla con el fondo del editor de la pregunta y la pregunta que está en negro no la ves porque tienes que bajar hacia abajo con la rueda del ratón (esto antes de enviar tu pregunta).
2) El tamaño de la imagen es inadecuado (hazla más grande).
3) El formato de la imagen es inadecuado (intenta que sea jpg,png...).
4) El internet te va muy lento (espera a que cargue la imagen).
5) No la adjuntas bien, pulsa en el icono de la imagen y luego pulsa en seleccionar desde los archivos. (no la arrastres encima).
En todo caso, aunque no se vea la miniatura de la imagen, ésta se puede ver al apretar encima. Así que no te preocupes si no te contestan, que la pregunta sí que la vemos.
Un saludo.
-
David Sánchez
el 2/9/16Hola tengo una duda: Un grupo de alumnos formado por veinte chicas y diez chicos organizan un viaje. Para que el viaje les salga más económico decide pedir trabajo por las tardes en una compañía que se dedica a realizar encuestas y que contrata a equipos de jóvenes de dos tipos:
Tipo A: Parejas (una chica y un chico).Tipo B: Equipos de cuatro (tres chicas y un chico)La compañía paga 30 euros por la tarde de la pareja y 50 euros por la tarde del equipo de cuatro.a) ¿Cómo les conviene distribuirse para sacar la mayor cantidad posible de dinero?b) ¿Y si les pagara 30 euros por la tarde de la pareja y 30 euros por al tarde del equipo de cuatro?Jordi García
el 2/9/16Hola David.
a) Yo he deducido que si no sobra ningún alumno el beneficio será mayor, por tanto he hecho:
x = número de grupos de 4 ; y= número de parejas
20 - 3x = 10 - x → -3x + x = 10 - 20 → -2x = -10 → x = 5 grupos
20 - 3x = 5 → Sobran 5 chicos
10 - x = 5 → Sobran 5 chicas.
Por tanto, se pueden hacer 5 parejas → y = 5 parejas
a) Les conviene distribuirse en 5 grupos y 5 parejas para sacar la mayor cantidad de dinero posible (400€).
b) Si les pagan lo mismo con una pareja que con un grupo, lo lógico es que hagan todas las parejas posibles:
Beneficio:
Todas las parejas posibles: 10 · 30€ = 300€ (Sobran 10 chicas).
Máximo número de parejas y grupos: 5 · 30€ + 5 · 30€ = 300€ (No sobra nadie).
Todos los grupos posibles: 6 · 30€ + 2 · 30€ = 240€ (Sobran 2 chicos).
b) Les convendrá distribuirse en 10 parejas para sacar la mayor cantidad posible de dinero y trabajar menos (300€).
Espero que te sirva, un saludo.
-
Marco
el 2/9/16
-
Marco
el 2/9/16 -
Sus
el 2/9/16Hola Unicoos,
paso a paso, como resolverian esta ecuacion?
Gracias
César
el 2/9/16Sus
el 2/9/16 -
Jordi García
el 2/9/16Hola UNICOOS, ¿podrían ayudarme en el siguiente ejercicio ? (IMAGEN ADJUNTA)
Gracias chic@s.
-
Sus
el 2/9/16Buenas,
si alguien puede explicarme porque con lamda 1⁄8, los valores propios son 0 y 3⁄2.
Se lo agradezco.
saludos
-
Juan
el 2/9/16Hola:
Tengo el siguiente problema de programación lineal y ya estoy mareado, ¿alguien puede ayudarme?
Una empresa ganadera puede producir novillos para exportación y novillos para el mercado interno a partir de una dieta proveniente de dos recursos forrajeros convencionales (pastura 1 y pastura 2) y un alimento concentrado. Se evalúa la duración del ciclo productivo completo (desde la compra del “destete” hasta el engorde completo del novillo) en un año. La empresa está sujeta a restricciones en cuanto a la disponibilidad de tierra y de capital operativo. Las necesidades nutricionales se evalúan a partir de los requerimientos de proteína cruda, fibra cruda y energía neta por animal y los suministros nutricionales a partir de la disponibilidad de los mismos componentes o elementos. Se desea obtener a partir del desarrollo y resolución de un modelo (problema) de programación lineal el valor del margen bruto de la empresa (valor de la función objetivo), el uso de recursos (superficie de las pasturas y toneladas de concentrado) y la cantidad y tipo de novillos destinados a la venta. La alta disponibilidad de fibra del concentrado posibilita que cualquier combinación alimentaria sea factible.
El problema debe ser resuelto a partir de la siguiente información técnica y económica:
(1) El margen bruto que proporciona el engorde de un novillo para exportación en un año es de 17 unidades monetarias (evaluadas en 1 mil pesos por cada unidad monetaria para simplificar la presentación).
(2) El margen bruto que proporciona el engorde de un novillo para mercado interno en un año es de 12 unidades monetarias (evaluadas en 1 mil pesos por cada unidad monetaria para simplificar la presentación).
(3) El costo directo de la producción/mantenimiento de 1 ha de la pastura 1 en un año es de 3.3 unidades monetarias.
(4) El costo directo de la producción/mantenimiento de 1 ha de la pastura 2 en un año es de 2.4 unidades monetarias.
(5) El costo de adquisición del concentrado es de 12 unidades monetarias por ton.
(6) Se considera que los novillos no ocupan espacio útil para simplificar la resolución del problema y que el almacenamiento de concentrado tampoco ocupa espacio útil en el establecimiento.
(7) El requerimiento de capital operativo de 1 novillo de exportación es de 0.8 unidades monetarias (adquisición de destete, sanidad, manejo del ganado).
(8) El requerimiento de capital operativo de 1 novillo para mercado interno es de 0.74 unidades monetarias (adquisición de destete, sanidad, manejo del ganado).
(9) Los requerimientos nutricionales de cada novillo de exportación durante 1 año (1 ciclo productivo completo) son de (a) 402 kg de proteína cruda, 475 kg de fibra cruda, 4900 mcal de energía neta.
(10) Los requerimientos nutricionales de cada novillo para mercado interno son de (a) 365 kg de proteína cruda, 410 kg de fibra cruda, 4015 mcal de energía neta.
(11) Los suministros nutricionales de cada 1 (una) ha de pastura 1 durante un año o ciclo productivo son de (a) 600 kg de proteína cruda, 900 kg de fibra cruda, 6300 mcal de energía neta.
(12) Los suministros nutricionales de cada 1 (una) ha de pastura 2 durante un año o ciclo productivo son de (a) 500 kg de proteína cruda, 1000 kg de fibra cruda, 6200 mcal de energía neta.
(13) Los suministros nutricionales de cada 1 (una) ton de concentrado son de (a) 200 kg de proteína cruda, 150 kg de fibra cruda, 2400 mcal de energía neta.
(14) La disponibilidad total de tierra es de 1000 ha.
(15) La disponibilidad total de capital operativo durante 1 año o ciclo productivo es de 500 unidades monetarias.
(16) Se solicita resuelva el problema a partir de estos datos.
·
· X1= producción de novillos ( E+ I)
· X2= pasturas ( 1 + 2)
· X3= alimento concentrado
· X4= requerimientos nutricionales( proteína cruda, fibra cruda y energía neta)
Restricciones
· Tierra ( r1)
· Capital ( r2)
Disponibilidad total de tierra (r1)= 1000 has
Disponibilidad total de capital (r2)= 500 UM
Valores correspondientes
C1 (margen bruto total de novillos exportación + mercado interno)= 17+ 12=29
C2 (costo directo total de producción/ mantenimiento pastura 1 + pastura 2)= 3,3 UM+ 2,4 UM = 5,7 UM
C3 (costo adquisición del concentrado)= 12 UM
C4 (requerimientos nutricionales para el total de novillos)= novillo exp. (402+475+4900) + novillo int. (365+ 410+ 4015) = 5777+4790= 10.567
C5 (requerimientos nutricionales para el total de pasturas = pastura 1 (600+ 900+ 6300) + pastura 2 (500+ 1000+ 6200)= 7800+7700= 15.500
C6 (requerimientos nutricionales del alimento concentrado= 200+150+2400=2.750
(17) Se considera que los novillos no ocupan espacio útil para simplificar la resolución del problema y que el almacenamiento de concentrado tampoco ocupa espacio útil en el establecimiento.
(18) El requerimiento de capital operativo de 1 novillo de exportación es de 0.8 unidades monetarias (adquisición de destete, sanidad, manejo del ganado).
(19) El requerimiento de capital operativo de 1 novillo para mercado interno es de 0.74 unidades monetarias (adquisición de destete, sanidad, manejo del ganado).
Función Objetivo= max el MB (valor total de los novillos- costo directo de las pasturas- costo concentrado).
