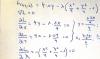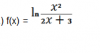EN LA ULTIMA ECUACIÓN NO TIENES A .λ  , PUESTO QUE PUEDES DESPEJAR A X O A Y , LUEGO SUSTITUYES EN LAS DOS PRIMERAS QUEDÀNDOTE UN SISTEMA DE 2 ECUACIONES CON DOS INCÒGNITAS ..

AQUÌ TE VA UN EMPUJÒN , CREO QUE IBAS POR ESTE MISMO CAMINO PERO A LO MEJOR PENSASTE QUE NO !! EL RESTO, LO REMATAS TÙ , NOS CUENTA VALE!!

Hola, Juan. Recordemos que si tenemos una función derivable u y queremos derivar Ln(u), queda u'/u; por ejemplo, f(x) = ln(x), f'(x) = 1/x. Así, para derivar tu función habría que hacer u = (x^{2})/(2x+3). Observa que u es una función racional, del tipo P/Q, por lo que su derivada es (P'Q-Q'P)/Q^{2}. Espero que con estas pistas te salga. ;)

AHÌ TE VA UNA AYUDITA PUES .. APROVECHA!!

Comencemos por expresar la ecuación de la superficie (S) en forma implícita:

3xy + z^2 - 4 = 0

observa que S es una superficie de nivel de la función: F(x,y,z) = 3xy + z^2 - 4, que es una función diferenciable en R^3, por lo que admite plano tangente en cualquiera de sus puntos, cuyo vector normal en cada caso puede ser calculado evaluando el vector gradiente de la función. El vector gradiente queda planteado:

gradF = < 3y , 3x , 2z >.

Luego, pasamos a los puntos:

(1,1,0) y (0,0,0) no pertenecen a S, ya que sus coordenadas no verifican la ecuación.

(1,1,1) si pertenece a S, porque sus coordenadas si verifican la ecuación, por lo tanto el vector normal al plano tangente a S en este punto será:

gradF(1,1,1) = < 3 , 3 , 2 >.

Luego, planteamos la ecuación cartesiana del plano tangente en este último punto:

3(x - 1) + 3(y - 1) + 2(z - 1) = 0

distribuimos, reducimos términos semejantes y queda:

3x + 3y + 2z - 8 = 0.

Espero haberte ayudado.

EL ANGULO 250 SE ENCUENTRA EN TERCER CUADRANTE, PUESTO QUE SU COSENO ES NEGATIVO..  SI LO REDUCIMOS AL PRIMER CUADRANTE , ENTONCES TENEMOS QUE : 250-180= 70 . POR LO QUE: COS (250) = -COS(70) = -0.34)

Y EL ANGULO DE 290 PERTENECE AL CUARTO CUADRANTE , VIENE REPRESENTADO POR SU MISMO RADIO VECTOR QUE EL ANGULO -70, POR LO QUE:

COS 290 = COS(-70)

COS(-θ)=COS(θ)

ENTONCES: COS 290 = COS(-70)= COS 70 = 0.34

EPA GABRIEL , DE DONDE SACAS QUE COS(70+3*60) = COS70+3*COS60 , ESTAS APLICANDO PROPIEDAD DISTRIBUTIVA EN RAZONES TRIGONOMETRICAS ? POR QUE SI ES ASI , ENTONCES ES FALSO LO QUE DICES!!

Daniel, es verdad... Lo he borrado antes de causar algún follón a alguien... Espero que Pau no me haya leído xD

Gracias Daniel.

JAJAJAAJ , TRANQUILO  HERMANO YO TAMBIÈN ME HE EQUIVOCADO BURDA!! .. PARA ESO ESTAMOS!!

HOLA SUS,  EN LA SEGUNDA INTEGRAL , ES   ∫x²dy+∫y²dy=x²y+(y³/3)+B(x)  

y entonces B(x)= ?

Gracias.

ESO ES LO QUE PARECE EXTRAÑO , POR QUE AGREGASTE B(X)? , SEGUN LA DEFINICIÒN DE LA ECUACIÓN DIFERENCIAL EXACTA SERIAN CUATRO PASOS: PRIMERO: HALLAR ∫Pdx+g(y)

SEGUNDO: d( ∫Pdx)/dy+g`(y)=Q

TERCERO: HALLAS g(y) INTEGRANDO g`(y)

CUARTO: ∫Pdx+g(y) =c  SERIA LA SOLUCIÒN 

INTENTALO DE ES MANERA!!

Hola algun unicoo que conozca mi metodo expuesto de resolcuion de ec. exactas
 ?

LA TIENES BIEN , NO VEO NINGÙN ERROR , ESO QUE ESTÀ EN ROJO NI YO MISMO LO ENTIENDO.

No comprendo por qué hiciste y' = 0 (creo que es lo que tienes incorrecto en la azul). Lo que está hecho en rojo es (2-xy)' = -xy' seguido de  las correspondientes cuentas posteriores. 

MACU: SE HIZO Y`=0 POR QUE SE ESTÀ DERIVANDO CON RESPECTO A X , POR LO QUE LA Y SE CONSIDERA CONSTANTE ..

Sospecho algún error o alguna omisión en el enunciado, Rodrigo:

HOLA CESAR!!! , OBVIAMENTE EL PUNTO A ESTÀ EN LA RECTA PERPENDICULAR r , YA QUE SU SIMÉTRICO TAMBIÉN LO ESTA, TE RECOMIENDO QUE VEAS LOS VIDEOS DE DAVID BUSCALOS , TE PASARA EL ENLACE DEL VIDEO DE DAVID PERO CREO QUE LA PAGINA ESTA MANTENIMIENTO Y HAY ALGUNAS FUNCIONES COMO POR EJEMPLO ESA QUE NO ESTA DISPONIBLE .. , ALLÌ SALE PASO A PASO QUÈ HACER EN ESTE TIPO DE EJERCICIOS ..SALUDOS 

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

Para que un subconjunto sea subespacio vectorial se ha de cumplir que cualquier combinación lineal de elementos de él esté también en el. Esto incluye:

Que esté el vector nulo. Que esté el opuesto. Que esté el producto de un escalar por un vector. Y que esté la suma y la resta de vectores pertenecientes a dicho subconjunto.

En este caso hemos encontrado  dos polinomios de A cuya resta no está en A. 

Espero haberte ayudado, Sandro.

Revisa la definición de subespacio vectorial y recuerda que el requisito principal es que A sea espacio vectorial de por si. Coge A y revisa las propiedades que verifica o no una a una. ;)

HOLA!! , SOLO DEBES MIRAR BIEN LAS ECUACIONES VECTORIALES , Y PENSAR QUE SE PUEDEN FORMAR SISTEMAS DE ECUACIONES PARA HALLAR LAS COORDENADAS DE LOS VECTORES u y v .. TE AYUDAMOS EN LO MAS DIFICIL , EL RESTO CORRE POR TU CUENTA ..