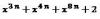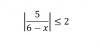-
Holaaa tengo un examen en unas horas y me acaban de surgir unas dudas... en un sistema de inecuaciones por ejemplo: --X > 8 si quiero cambiar el signo de x para que sea positivo se quedaía así: X < -8 ???
EL RESULTADO DEL EJERCICIO 2 ES: { 2, 8 } O ES {2,-8}
Y EL EJERCICIO 3 NO SE COMO HACERLO, POR FAVOR SI ALGUIEN PUEDE AYUDARME!

Jordi García
el 2/9/16Hola KD, aunque ya hayas hecho el examen te envío las soluciones:
En el ejercicio 2 la solución es (-∞,-8] U [2,+∞).
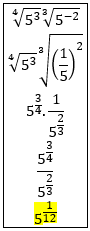
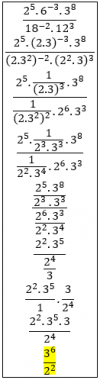
En el ejercicio 3 las soluciones son:
a) 36 /22
b) 12√5
Si no consigues llegar a las soluciones mira vídeos de dominios (ej.2) y de operaciones con radicales (ej.3).
Un saludo.
-
Hola, buenos días , me podrían ayudar a resolver este problema, hicimos ejemplos en clase sobre el tema de la ecuación de Lagrange, y se que se tiene que plantear la función objetivo (FO) y las funciones de restricción (FR) , pero todavía no me queda claro cuales son en este problema, primero pensé en poner a la FO como las hipotenusas (las cuales resultan ser las distancias) que sumadas dieran cero para obtener el mínimo costo, luego vi que de alguna manera tenia que incluir los 10 km. y ya super que hacer, ademas a las FR las puse como distancia PQ-3k=0, QR-2K=0, RS-K=0 pero no creo que este correcto. Por favor alguien podría ayudarme a plantear solo las funciones y yo podre realizar el resto. Gracias
-
Hola,
me pueden explicar por pasos esta division de ecuaciones.?
Como resolverian ese sistema de ecuaciones?
Gracias
graci
alguien entiende de esto?
lambda = 8, que no aparece en la solucion del ejercicio, tambien adjunto, por lo que he supuesto que ya iba mal.
Hola, necesito ayuda para comprender el orden adecuado para resolver sistemas de ecuaciones de varias incognitas, y sacar todos los puntos posibles. os adjunto mi ejercicio en el que paré cuando saque un
-
Hola UNICOOS, aquí va mi pregunta:
¿Qué relación existe entre la tangente de dos ángulos suplementarios, complementarios, opuestos, que difieren en π y que difieren en π/2?
-


Nenúfar
el 2/9/16Es X elevado a 8n.
Si te das cuenta n puede tener cualquier valor, ponle el número que quieras para que te resulte más fácil.
Si n es siempre el mismo número, tendrá mayor grado aquel monomio que tenga un exponente mayor, puesto que el resultado de la potencia será mayor.
Por ejemplo, si suponemos que n es 2 (es un ejemplo) quedaría X^6+ X^8+X^16+2. (solo se sustituye la n por un dos)
y de todos esos exponentes el mayor es 16. El correspondiente al monomio X^8.
Espero haberte ayudado y que hayas comprendido bien la respuesta.
Suerte con tus estudios Renato:)
PD:; Este signo ^ significa exponente, pos si no lo sabías.
-


Nico
el 2/9/16Si la base de salida es B1={ (1,1,1),(1,1,0),(1,0,0)}
Las columnas de la matriz asociada, son las coordenadas de la transformación de los vectores de la base de salida en la base de llegada, por tanto:
T(1,1,1)= (4,2,4) T(1,1,0)= (3,2,2) T(1,0,0)= (2,0,1)
Ahora tenes que hallar los vectores en la base de llegada:
T(1,1,1)= 4(1,0,0) + 2(0,1,0) +4(0,0,1) = (4,2,4) (como te darás cuenta las coordenadas, son las componentes del vector, ya que la base es la canónica,) por tanto:
T(1,1,0)= (3,2,2)
T(1,0,0)= (2,0,1)
ahora para hallar la ecuación de la de TL planteas que como {(1,1,1),(1,1,0),(1,0,0)} conforman una base, cualquier vector se puede expresar como CL de ellos, en particular el vector (x,y,z)
a(1,1,1)+b(1,1,0)+c(1,0,0)=(x,y,z)
te quedará un sistema de 3 ecuaciones:
a+b+c=x
a+b=y
a=z despejando de la segunda ec. te queda b= y-z
sustituyendo en la primera ec. z +y-z +c= x
despejando: c=x-y
Por otro lado planteamos T(x,y.z)= aT(1,1,1)+bT(1,1,0)+cT(1,0.0)
Ahora sustituimos los T (1.1.1), T(1,1,0).T(1,0,0) por los vectores correspondientes a cada uno, y ademas sustituimos los valores a,b,c
T(x,y,z)= z(4,2,4)+(y-z)(3,2,2)+(x-y)(2,0,1)
y de aqui aplicamos distributiva..
T(x,y,z)=(z+y+2x, 2y, 2z+y+x)


Nico
el 2/9/16Para el rango:
Planteas (2x +y +z, 2y ,x+y+2z)= x (2, 0 ,1)+ y(1, 2 ,1)+ z(1, 0, 2) los vectores {(2,0,1),(1,2,1),(1,0,2)} son generadores de la imagen de T, en particular una base, #B=3 por tanto el rango es 3
Para el kernel de T iguala las ecuaciones a cero y despeja x en funcion de las otras dos variables luego y y lo mismo con z , despues de eso el proceso para calcular la base es análogo al de la imagen
Cualquier cosa pregunta de nuevo!
Saludos!!
-


Emiliano
el 2/9/16Si, yo llegué a ese mismo resultado. Pero creo que eso no es correcto, ya que según ese resultado, x solo puede tomar valores menores o iguales a 3,5 para que se cumpla la condición planteada. Ahora bien si x toma un valor mayor a 3,5, por ejemplo el x=10, nos quedaría:
|5/(6-10)|≤2
|5/(-4)|≤2
|-1,25|≤2
o sea
1,25≤2
Por lo que se esta cumpliendo la condición, aunque x tome un valor mayor a 3,5.


Antonio Silvio Palmitano
el 2/9/16Observa que podemos distribuir el valor absoluto, y que x no puede tomar el valor 6. Luego la inecuación queda:
5 / |6 - x| <= 2, como el divisor es positivo (es un valor absoluto) hacemos pasaje y queda:
5 <= 2|6 - x|, hacemos pasaje del factor numérico como divisor y queda:
5/2 <= |6 - x|, observa que la inecuación es equivalente a:
|6 - x| >= 5/2, luego por propiedad del valor absoluto con desigualdad tenemos dos opciones:
a)
6 - x >= 5/2, hacemos pasaje de término y resolvemos a la derecha y queda:
-x >= -7/2, luego multiplicamos por -1 en ambos miembros (observa que se invierte el sentido de la desigualdad) y queda:
x <= 7/2, que es parte de la solución.
b)
6 - x <= - 5/2, hacemos pasaje de término y resolvemos a la derecha y queda:
-x <= -17/2, luego multiplicamos por -1 en ambos miembros (observa que se invierte el sentido de la desigualdad) y queda:
x >= 17/2, que es la otra parte de la solución.
Por lo tanto, la solución es:
x pertenece a (-inf , 7/2] u [17/2 , +inf) con notación de intervalo.
Espero haberte ayudado.
-
Holaa compañeros de unicoos, me podrian ayudar con este ejercicio de ecuaciones vectoriales :
A+3B-C= (1,1,1),
2A-B+4C=(0,1,-3) ,
A+2B-2C= (4,2,1) ,

Daniel González
el 1/9/16EPA ALEX!! BUENO MI HERMANO , COMIENZA DEFINIENDO LAS COORDENADAS DE CADA VECTOR , ASÌ!!
SEAN : A=(A1,A2,A3) ; B=(B1,B2,B3) ; C =(C1,C2,C3)
LUEGO SUSTITUYELAS EN CADA VECTOR:
(A1,A2,A3)+3(B1,B2,B3) -(C1,C2,C3)=(1,1,1) →(A1+3B1-C1 , A2+3B2-C3 , A3+3B3-C3)=(1,1,1)
2(A1,A2,A3)-(B1,B2,B3) +4(C1,C2,C3)=(0,1,-3) →(2A1-B1+4C1 , 2A2-B2+4C2 , 2A3-B3+4C3)=(0,1,-3)
(A1,A2,A3)+2(B1,B2,B3) -2(C1,C2,C3)=(4,2,1)→(A1+2B1-2C1 , A2+2B2-2C2 , A3+2B3-2C3)= (4,2,1)
SE FORMAN TRES SISTEMAS DE ECUACIONES C0N TRES INCOGNITAS:
A1+3B1-C1=1 A2+3B2-C3=1 A3+3B3-C3=12A1-B1+4C1=0 2A2-B2+4C2=1 2A3-B3+4C3=-3
A1+2B1-2C1=4 A2+2B2-2C2=2 A3+2B3-2C3=1
TE SUGIERO QUE TE PREPARES UN BUEN CAFÈ, Y TE FAJES .. NOS CUENTAS OK..
-
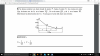
Hola profesores tengo una duda, quería que me explicaran de a donde salio el 7.5 en este ejercicio ya resuelto, y también quería saber ¿cuales son las coordenadas de los puntos donde el círculo de riego es tangente al terreno?, ya que no entiendo, de ante mano muchas gracias


Daniel González
el 1/9/16HOLA MARIANO, CON RESPECTO A LA PRIMERA DUDA : LAS COORDENADAS DE CENTRO SON : (7,5, 5) ESTO ES POR QUE LA COORDENADA X DEL CENTRO DEL CIRCULO, ES EL PUNTO MEDIO DEL LADO MAS LARGO, Y COMO EL LADO MIDE 13 , ENTONCES 13/2 = 7,5 . LO MISMO PASA CON LA COORDENADA EN Y DEL CENTRO, EL LADO MIDE 10 , EL CENTRO ESTA EN LA MITAD , POR LO TANTO SERIA 5 . CON RESPECTO A LA SEGUNDA DUDA: LAS COORDENADAS DE LOS PUNTOS DONDE EL CIRCULO ES TANGENTE AL RECTÀNGULO SERIAN (7,5,10) Y (7,5,0). YA QUE EN ESE PUNTO EL CIRCULO ES TANGENTE EN JUSTAMENTE LA MITAD DEL LADO MAS LARGO DEL RECTANGULO .. ESPERO QUE MI EXPLICACIÒN TE HAYA SERVIDO DE ALGO..