-
Hola a todos. Me dieron una tarea, y no estoy seguro si está bien, alguien me podría confirmar si está bien o mal?
Dibujar una gráfica de una función con dominio en los reales, con conjunto de positividad igual a su dominio, derivable en los reales que satisfaga las siguientes condiciones:
F(0) = 3
F(x) es par
F´(3) = 0
F´´(x) es menor que 0 Para todo X perteneciente al intervalo (0,1)
F´´(x) es mayor que 0 Para todo X perteneciente al intervalo (1 ; +infinito)
Muchas Gracias!
-
-
Hola!
Me pueden corregir por favor el problema?
Dado el programa,
optimización x+z
sujeto a x²+y²+z²=1
sus puntos óptimos son: (−√2/2, 0, −√2/2; −√2/2) que es un máximo y (√2/2, 0, √2/2; √2/2) que es un mínimo.

Antonio Silvio Palmitano
el 8/8/16Los puntos críticos son (L indica "lambda"):
P1(−√2/2, 0, −√2/2), cuyo multiplicador es L1 = −√2/2 que es distinto de cero, y f(−√2/2, 0, −√2/2) =-V(2)
P2(√2/2, 0, √2/2), cuyo multiplicador es L2 = V(2)/2 que es distinto de cero, y f(√2/2, 0, √2/2) = V(2).
El teorema de Lagrange garantiza extremos absolutos, por lo tanto la función alcanza Máximo Absoluto en P2, y mínimo Absoluto en P1.
Espero haberte ayudado. -
Hola Unicoos,
alguien podría decirme si estoy en lo cierto cuando digo que los puntos críticos de la función, f(x,y )= (x−1)²−y(y−2) son extremos absolutos?
Le he dado vueltas pero es muy complicado...

Antonio Silvio Palmitano
el 8/8/16Vamos con la función, cuya expresión puede escribirse:
f(x,y) = (x - 1)^2 - y^2 + 2y
sus derivadas primeras son:
fx = 2(x - 1)
fy = -2y +2
Planteamos la condición de punto estacionario:
2(x - 1) = 0, de donde tenemos: x = 1
-2y + 2 = 0, de donde tenemos: y = 1
observa que las ecuaciones son independientes (no comparten incógnitas), por lo tanto el punto estacionario es: Po(1,1)
Vamos con sus derivadas segundas:
fxx = 2
fxy = 0
fyx = 0
fyy = -2
observa que son todas constantes, por lo que pasamos directamente al discriminante y tenemos:
D = 2*(-2) - 0*0 = -4 <0.
Por el criterio de las derivadas segundas, tenemos que la gráfica de la función presenta un punto de ensilladura en Po(1,1), y f(1,1) = 1.
Por medio de un graficador, podrás observar que la gráfica de la función es un paraboloide hiperbólico, con Centro en el punto de coordenadas (1,1,1).
Espero haberte ayudado. -
La ecuación 6x^3 + 11x^2 = 3x +2 la hago a través de ruffini y las raíces me dan -1/2 y 1/3 me podrían decir si está bien?
-
En una oposición un ejercicio versa sobre 50 posibles temas. Si seleccionamos al azar 3 bolas y el opositor elige dos de los temas seleccionados para los que debe demostrar un conocimiento completo. Si se ha estudiado bien 30 de esos 50 temas. ¿Qué probabilidad habrá de aprobar?¿Cuántos temas que conocer para que la probabilidad de aprobar sea de al menos el 80%?
La probabilidad de aprobar sería así: -
Hola unicoos me podría alguien ayudar con este problema de vectores??no entiendo como relaciona el teorema del coseno con el ángulo de 144°,no esta dentro de ningun triángulo,gracias de antemano










_Thumb.jpg)


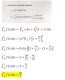

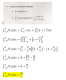
_Thumb.jpg)

_Thumb.jpg)


_Thumb.jpg)



