-
Hola buenos días, disculpen las molestias nuevamente. tengo que hacer la ecuación parametrica del plan o, me dan un punto que pertenece a la recta y un vector paralelo... la duda mía es ¿como consigo el vector que me falta para poder formarla o con un solo vector alcanza?
Ejercicio:
Hallar ecuación parametrica de la recta paralela al vector u=2i+j-k que pase por el punto M(2,0,3)
yo había hecho lo siguiente
x=2+2t
y=t
z=-1+3t
y luego recordé que se necesitan 3 términos dentro de cada ecuación, es decir 1 punto y 2 vectores.
Desde ya muchas gracias, saludos.
Feli Gariboldi
el 8/8/16Gracias Antonio, si me exprese mal yo.
y supongamos que después tengo que ver si el punto R (3,1/2, 5/2) esta en dicha recta, ¿que hago? ¿hago la ecuación general del vector dado con el primer punto (2,0,3) me fijo el valor del termino independiente y después hago lo mismo con el punto R? es decir:
2.2-3 + D =
D=-1
y luego :
2.3+1/2-5/2 +D =
D =4
por lo tanto dicho punto no pertenece a la recta porque los términos independientes son de distinto valor.
¿correcto? -
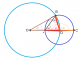
Hola chicos, alguien podria explicarme como se hace este ejercicio, me he quedado un poco atascado, gracias.
-
Hola amigos de unicoos, les pido ayuda con estos problemas, solo deseo ayuda con el 7 y el 9
Gracias -


Andrés Alvarado
el 8/8/16Hola tomas, te dibuje con los circulos para que notes que los triangulos BAD y BOD son triangulos isosceles debido a que tienen dos lados iguales y son iguales por que son los mismos radios de la circunferencia, recordandote que en un triangulo iscoceles dos de sus lados y angulos son iguales y tambien recordandote que la suma de los angulos internos de un triangulo es siempre 180, espero ayudarte tomas suerte :) La respuesta es 20
-
Holaa, me ayudan con este ejercicio? yo mas o menos lo resolví y me dió que para que sea Indeterminado k=6, para que sea Compatible determinado k=3, y para que sea Incompatible k=2. Pero creo que no está bien..
-
Unicoss resolví esta integral ∫ dx/√(4+x²) y me dio como respuesta ln|√(4+x²)/2+x/2|+C. Quiero saber si mi resultado es correcto la resolví con cambio de variable trigonometrica y según el resultado de la guia me tendria q ver dado ln|√(4+x²)+x|+C. Cual esta correcta????


Antonio Silvio Palmitano
el 8/8/16La sustitución a aplicar es:
x = 2tanu, de donde tenemos: dx = 2 *dx / (cosu)^2, y también: 4 + x^2 = 4/ (cosu)^2, cuya raíz cuadrada queda: 2/cosu.
Vamos con la integral, sustituimos, simplificamos y queda:
I = Integral (1/cosx)*dx = Integral (cosx / (cosx)^2)*dx = Integral (cosx / (1 - (senx)^2))*dx
Luego, una nueva sustitución:
w = senx, de donde tenemos: dw = cosx*dx, sustituimos y queda:
I = Integral (1 / (1 - w^2))*dw
Esta integral se puede resolver con el método de las fracciones parciales, ya que:
1 / (1 - w^2) = 1 / (2*(1 + w)) + 1/(2*(1 - w))
Luego reemplazamos, integramos y queda:
I = (1/2) * ln|1 + w| + (1/2) * ln|1 - w| + C.
Solo resta volver a sustituir:
a partir de u = senw, tenemos que: w = arcsenu,
y luego:
a partir de x = 2tanu, tenemos que: u = arctan(x/2)
Espero haberte ayudado.
Xavi
el 8/8/16Si X=2tgθ. dx=2sec²θdθ
Entonces 2∫sec²θ/√4+(2tgθ)²= 2∫sec²θ/√4+(4tg²) factorizamos el denomonador = 2∫sec²θ/√4(1+tg²θ)
Sacamos ese cuatro de la integral y se elimina con el dos= ∫sec²θ/√(1+tg²θ) y esto es igual a ∫sec²θ/√sec²dθ se elimina la raiz con el cuadrado y nos queda ∫sec²θ/secθ ∫secθdθ =ln|secθ+tgθ|+c.
Luego regreso a mi variable original q es X.
-
Hola Unicoos! Si alguien sabe del tema extremos relativos y absolutos y Lagrange, me puede ayudar con el ejercicio 8 y 9 b)? Muchas gracias!!!
-
Sea f(x)= 5x +3 y g(x) una función cualquiera derivable en x=8. sabiendo que (g o f )´ (1) = 2 . Calcular g´(8)


Antonio Silvio Palmitano
el 8/8/16Observa que f es una función derivable, que f(1) = 8, y también que f ' (x) = 5 (observa que la derivada de la función f es constante).
Luego, vamos con la función compuesta: (g o f)(x) = g(f(x)), que es la función que debemos derivar y evaluar.
Luego, aplicando la regla de la cadena tenemos:
(g o f) ' (x) = g ' (f(x)) * f ' (x)
Luego evaluamos para x = 1 y nos queda:
(g o f) ' (1) = g ' (f(1)) * f ' (1) = g ' (8) * 5
Por último, empleando el dato de la función compuesta evaluada que nos brinda el enunciado tenemos:
2 = g ' (8) * 5
despejamos y llegamos a:
2/5 = g ' (8).
Espero haberte ayudado.





















_Thumb.jpg)






_Thumb.jpg)
