-
Hola a todos. Me dieron una actividad para resolver, y hay una parte en que ya no sé cómo resolverla.
La actividad es la siguiente, dado la función F(x), ¿se puede aplicar el teorema de lagrange en el intervalo cerrado menos dos quintos; tres medios?
En caso negativo explicar por qué. En caso afirmativo calcular el o los valores “C” que satisfagan el teorema.
Lo primero que hice, es averiguar si F(x) era continua y derivable, más que nada en los puntos 1 y 2 que es en donde tenía dudas. Llegue a la conclusión que F(x) es continua y derivable, porque además el intervalo cerrado menos dos quintos; tres medios, se encontraba dentro de la función.
Yo lo que tenía pensaba era reemplazar el -2/5 en X al cubo menos x, y el 3/2 cuando la función vale 2(x-1). De esa manera encuentro los valores de F(b) y F(a),
LO QUE NOCE COMO HACER, ES COMO ENCONTRAR LOS VALORES “C” QUE SATISFAGAN EL TEOREMA.
DE QUE MANERA ENCUENTRO LOS VALORES “C” QUE SAFISFAGAN EL TEOREMA?
Muchas Gracias.
-
Hola a todos los unicoos!
Ando atascado en un sistema de ecuaciones. Su resultado es (-1,2) y (-2,1), pero no consigo llegar a esa conclusión.
Lo primero que hago es despejar x de la primera ecuación, más sencilla y queda que x = y-3
Luego sustituyo la x en la segunda ecuación (y-3)²+y²=5
A partir de aqui, al hacer la identidad notable (me da 3) y resolver la ecuacion de segundo grado, me da +- raiz de 2.
Espero que algún unicoo vea lo que falta (o sobra), gracias unicoos!!
-
Hola a todos. Me dieron una actividad para resolver, y hay una parte en que ya no sé cómo resolverla.
La actividad es la siguiente, dado la función F(x), ¿se puede aplicar el teorema de lagrange en el intervalo cerrado menos dos quintos; tres medios?
En caso negativo explicar por qué. En caso afirmativo calcular el o los valores “C” que satisfagan el teorema.
Lo primero que hice, es averiguar si F(x) era continua y derivable, más que nada en los puntos 1 y 2 que es en donde tenía dudas. Llegue a la conclusión que F(x) es continua y derivable, porque además el intervalo cerrado menos dos quintos; tres medios, se encontraba dentro de la función.
LO QUE NOCE COMO HACER, ES COMO ENCONTRAR LOS VALORES “C” QUE SATISFAGAN EL TEOREMA.
DE QUE MANERA ENCUENTRO LOS VALORES “C” QUE SAFISFAGAN EL TEOREMA?
Muchas Gracias.

Sebastián
el 7/8/16hola antonio, es -2/5 a 3/2. La funcion es continua desde el -3/2 a 5/2, que es lo que demostre yo. Ahora bien, el intervalo -2/5 a 3/2 se encuentra dentro de la funcion. Osea, la funcion es continua y derivable, entonces lo que yo pensaba era reemplazar el -2/5 en X al cubo menos x, y el 3/2 cuando la funcion vale 2(x-1). De esa manera encuentro los valores de F(b) y F(a), luego no se como encontrar C.
-
hola unicoos me podrian ayudar con este problema de probabilidades ,por fabor. ......en un edificio de 10 pisos,entran al ascensor en el primer piso,3 personas si cada una baja en un piso diferente a partir del segundo piso,de cuantas maneras disitintas estas personas se podran bajar?.......que puedo usar una variacion oh una combinacionnnnnnn???????????


Antonius Benedictus
el 7/8/16Vamos a codificar la situación, Hugo. Supongamos distinguibles a las personas:
A (baja la primera), B (baja la segunda), C (baja la tercera), 0 (no baja nadie)
Si cada una baja en un piso diferente:
(A,B,C,0,0,0,0,0,0,0)
.....
(0,0,0,0,0,0,0,B,C,A)
Serían permutaciones con repetición de 1, 1, 1 y 7. Esto es: 10!/(1!·1!·1!·7!)=10·9·8=720
Si consideramos iguales a las personas (A,A y A):
Permutaciones con repetición de 3 y 7. Esto es: 10!/(3!·7!)=10·9·8/6=120
-
Hola unicoos quien me ayuda con el siguiente problema:
El diámetro de una esfera es de 20 cm y se ha medido con una regla graduada que tiene un error menor que 0,1 cm. Indica el intervalo de valores posibles para el radio y para el volumen.

Francisco Gutiérrez Mora
el 7/8/16Bien:
Diámetro=D=20 ±0.1 cm=20.01; 19.99 cm
Volumen esfera= Ve=4/3πr³
Ve =4/3π20³=33503.32 cm² ( Supuesta cantidad sin error, con regla exacta)
Ve (con su error será: 4/3π·20.01³=33560.61 cm³ (Error por exceso)
Ve (con su error será: 4/3π·19.99³=33460.08 cm³ (Error por defecto)
Creo que es lo que pides: Un Saludo

Francisco Gutiérrez Mora
el 7/8/16Mariano, tengo que decirte que lo que te he expuesto son los errores máximos por defecto y por exceso que se cometerían aproximadamente si el error real de la regla fuera 0.1 cm. Esto no está hecho según Teoría de errores, pues con ella su tratamiento sería especial, nos darían una tolerancia máxima admisible, fuera de la cual no estaría permitido resultado alguno etc., etc.. Un Saludo.


Francisco Gutiérrez Mora
el 7/8/16Por eso te he puesto la segunda respuesta. Lo siento Mariano, yo no recuerdo bien este tipo de ejercicios, pues yo sólo soy ingeniero técnico, no soy profesor lo que pasa es me gustan bastante estas asignaturas. Un Saludo cordial amigo y créeme que siento de veras no haberte podido ayudar.
-
Hola, he planteado la resolucion de esta integral ∫(x²+2x-1)·senx dx en la foto adjunta.
Quisiera saber por favor si esta bien segun la formula de la integracion por partes que aparece en el recuadro.
Muchas gracias.

Antonio Silvio Palmitano
el 7/8/16En este caso, que podemos describir: "polinomio por seno", debes plantear:
u = función polinómica
dv = función trigonométrica*dx
aplicas el método, y en la integral secundaria, verás que queda: "polinomio por coseno", pero observa que el polinomio es un grado menor que el inicial, por lo que vuelves a aplicar el método de integración por partes:
u = función polinómica
dv = función trigonométrica*dx,
aplicas el método, y verás que la última integral a resolver es directa.
En tu ejercicio:
1° paso:
u = x^2 + 2x - 1, de donde tenemos: du = (2x +2)dx
dv = senx*dx, de donde tenemos: v = -cosx
Aplicamos el método (llamamos I a la integral original) y queda:
I = (x^2 + 2x -1)*(-cosx) - Integral (-cosx*(2x + 2)*dx)
luego resolvemos los signos en los términos y queda:
I = -(x^2 + 2x - 1)*cosx + Integral (cosx*(2x + 2)*dx
Ahora volvemos a aplicar el método en la integral secundaria (observa que volvemos a elegir al polinomio como primera función):
u = 2x + 2, de donde tenemos: du = 2dx
dv = cosx, de donde tenemos: v = senx
aplicamos, y la integral queda:
I = -(x^2 + 2x - 1)*cosx + (2x + 2)*senx - Integral(senx*2*dx) (observa que la última integral es de resolución directa).
Espero haberte ayudado -
Buenos días, Don Antonio Benito: En la pregunta que hace más abajo el amigo Mariano Michel, según el enunciado, ¿no está correcto mi dibujo y planteamiento?
Es que no me coinciden todas las coordenadas con las que usted propone. Un Saludo afectuoso, amigo. -
Hola!
no entiendo como lo hace para decidir que se pone un + donde puse el interrogante.
Y tampoco se que ley o propiedad es la que dice "que al ser una igualdad deben coincidir los coeficientes" y resulta que aparecen dos ecuaciones nuevas. Por que decide que el 5 hace ecuacion con (A+B), y no con el otro termino.No lo entiendo..
Agradeceria alguien me ayudara.

Antonius Benedictus
el 7/8/16Estamos hablando de "igualdad de polinomios" (en sentido funcional) y no de "igualdad entre números" (que sería una ecuación ordinaria).
Dos polinomios son iguales cuando:
Los términos independientes coinciden.
Los términos de primer grado ("en x") coinciden.
Los términos de 2º grado coinciden....
Etcétera.
Dos polinomios son iguales cuando:
Los términos independientes coinciden.
Los términos de primer grado ("en x") coinciden.
Los términos de 2º grado coinciden....
Etcétera.
">_Thumb.jpg)


Francisco Gutiérrez Mora
el 7/8/16Ana, lo único que se hace es agrupar términos: (5x-2)=Ax-2A+Bx+2B Si agrupamos tenemos que la x multiplica a A +B y el 2 multiplica a -A+B quedando en principio así:
5x-2=(A+B)x+2(-A+B) si cambiamos la A y la B de lugar podemos escribir: 5x-2=(A+B)x+2(B-A)
En cuanto a la coincidencia de coeficientes, al ser una igualdad, el coeficiente de la x sería: 5x=(A+B)x→5x/x=(A+B)→5=(A+B)
Por la misma razón de igualdad el término independiente de un lado de la igualdad debe ser igual al otro, por tanto -2=2(B-A)
Así lo he concebido, creo que es correcto lo que te explico. Un Salido, Ana.


_Thumb.jpg)




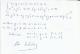


_Thumb.jpg)


_Thumb.jpg)




_Thumb.jpg)




_Thumb.jpg)







_Thumb.png)
