-
Augusto
el 3/6/16Ejercicio
Sea un valor real que esta estrictamente entre -1 y 1. Definimos la función siguiente de a. Demuestra que la función anterior solo se anula para un valor de x.
Podéis explicarme porque la derivada de esta función en función de a no tendrá solución teniendo en cuenta las condiciones del ejercicio?.
Antonio Silvio Palmitano
el 4/6/16Mira bien el argumento de la raíz cuadrada a la que has llegado, que es:
a^2 -1,
con la información del enunciado del problema, tenemos que:
-1 < a < 1, desigualdad que nos conduce a:
0 < a^2 < 1 (puedes visualizarlo con la gráfica de la función f(a) = a^2),
luego, por propiedad uniforme de las desigualdades, restamos 1 en cada miembro:
0 - 1 < a^2 - 1 < 1 - 1, que al resolver queda:
-1 < a^2 - 1 < 0, por lo que tenemos que el argumento de la raíz cuadrada es negativo, y la raíz no tiene solución en el conjunto de los números reales.
Ahora, como no tenemos puntos que anulen la derivada primera, tenemos que la función no presenta máximos ni mínimos, por que permanece monótona (siempre creciente en este caso, por el coeficiente principal de la expresión polinómica que es positivo).
Para concluir, si tomas límite a -infinito, verás que llegas a que la función tiende a -infinito, y si tomas límite a +infinito verás que tiende a +infinito y, como la función es continua para todos los números reales, tenemos que debe cruzar al eje de abscisas x en uno de sus puntos.
Espero haberte ayudado. -
Augusto
el 3/6/16Hay algún foro para tecnología industrial (nivel selectividad) o hay alguien del foro que entienda esta asignatura? Sobre todo la parte de máquinas (potencia útil, motor, par motor, rendimiento...)
Nico
el 3/6/16 -
GABRIELA
el 3/6/16Hola unicoos, pueden recomendarme algun libro o pdf de calculo diferencial e integral !!!!!!! es para estudiar teoria y demostraciones gracias !!!
-
Carlos
el 3/6/16Hola unicoos, les pidomde favor que me ayuden de nuevo con otra integral. No se si se puede hallar la respuesta en funcion de s, usando identidades de angulos dobles.
∫ (Tg 4s - Ctg (s/4)) ds por favor se los pidos. Gracias de antemano. -
Augusto
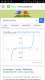
el 3/6/16Alguien me puede explicar por qué las derivadas de algunas funciones no tienen solución pero en cambio en la representación de la función se aprecia un punto de tangente horizontal?
Pongo la de la foto como ejemplo.
f'(x) no tiene solución pero en cambio se nota que cerca del origen tiene un punto de tangente horizontal.
Antonius Benedictus
el 3/6/16La derivada de esta función, efectivamente, no se anula. No hay punto de tangente horizontal en x=0. La función es creciente. Hay un punto de inflexión en x=0, pues la segunda derivada se anula y cambia de signo en en x=0. La escala con la que está representada la función provoca el engaño visual.
Augusto
el 3/6/16Me queda poco para pillarlo. Pero tengo aun una duda por despejar.
Según entiendo, en x=0 hay un crecimiento, y normalmente los crecimientos y decrecimientos se hallan con la derivada. Qué sucede en este caso? Podrías enseñarme una función en la que sea fácil de entender y ver un punto de inflexión sin derivadas?
Mi profesor de mates dice que cuando a punto crítico le precede un crecimiento y le sucede un crecimiento es porque hay un punto de inflexión, pero en este caso es que no se puede hacer la derivada para identificar los decrecimientos y crecimientos.
Lo siento por preguntar mucho, pero es que quiero pillarlo para hacer una buena selectividad.
Gracias.
Antonius Benedictus
el 3/6/16 -
Mariia
el 3/6/16Existe la inversa de una matriz 4x3 o 3x4? Es que tengo una duda con hacer AX=B siendo B 4x3...
¿Podrías ponerme un ejemplo de como se hace?Rodrigo
el 3/6/16
Nico
el 3/6/16Hola Maria, para resolver ecuaciones matriciales , tienes que multiplicar por la inversa de la matriz , a ambos lados de la ecuación para poder despejar la X, en tu caso no importa que la matriz B sea de 4x3 o 3x4 (obviamente siempre y cuando el producto de
B con la inversa de A sea conformable), lo que importa es que la matriz A sea cuadrada, para que pueda tener inversa..
Si seguis con dudas ,no dudes en preguntar.
Un saludo! -
andres
el 3/6/16
-
;-D
el 3/6/16Lanzamos tres dados igualmente trucados. Probar que la probabilidad de que la suma obtenida sea divisible entre 3 no es inferior a 1/4.
Usuario eliminado
el 5/6/16Va en dos entregas M-Terio,
¿De dónde sacas estos problemas que nos propones? No ha habido más remedio que trabajar con una función de dos variables. Date cuenta que al ser dados cargados es imposible relacionarlas y que al tener los tres dados la misma carga ha sido posible crear la función que nos da la probabilidad._Thumb.JPG)
-
Nico
el 3/6/16hola necesito ayuda con este ejercicio aun no entiendo la temática de los ejercicios de este tipo..hallar un generador del subespacio s
_Thumb.png)
Nico
el 3/6/16
Antonius Benedictus
el 3/6/16 -
Facundo Meier
el 3/6/16Hola como están?. Alguien me podrá ayudar a analizar la continuidad de la función en los reales. f(x)=e^1/x+1
Lo que hice fue calcular el limite de x tiende a uno por derecha y por izquierda y como el primero dio como resultado infinito, y el otro menos infinito, la funcion es Discontinua Escencial. Esta bien?
.jpg)
.jpg)
.JPG)
.JPG)
.png)
.jpg)
.jpg)
