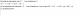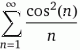-
Hola unicoos, disculpen podria algun experto ayudarme con dosnintegrales. ∫ (Sen x / Cos² x) dx y ∫ (Cos x/ Sen² x) dx
Me fustro ya que integrales no se me da muy bien como en las derivadas, pero espero mejorar en integrales siendo hábil cada vez.
Gracias de antemano.
Ignacio Pignanelli
el 23/5/16En ambas integrales tenés que usar sustitución .
Recordá que d/dx (cos(x)) = -sin(x) y d/dx(sin(x))=cos(x)
En la primera: u=cos(x) => du=-sin(dx) . Por lo tanto para que al reemplazar se trate de la misma función el integrando debe quedar: -du/(u^2) = (-1)*u^(-2) du, => la integral por regla de Barrow : 1/u + c. Volvés a reemplazar las u y te queda: 1/cos(x) + C. Espero que entiendas,no me sé explicar muy bien. -
El ejercicio es Lim x-> infinito (3x-28)´5 + (2x-21) / 25x´5 - 3x² +1
Lo resolvi dividiendolo entre la x con mayor potencia es decir x´5, sin embargo tengo una duda con este ejercicio si yo tengo el producto notable entre x´5 estamos hablando de cociente entre infinito o infinito sobre infinito.
(3x-28)´5 7 x´5 = 0 o (3x -28)´5 / x´5 = ∞ / ∞

David
el 23/5/16(3x-28)^5 no es un producto notable... Debes desarrollarlo... Lo ideal sería hacerlo aplicando el binomio de Newton... Binomio de Newton
A partir de ahí, te quedaría un limite del tipo ∞ / ∞ y el resultado rápido sería dividir el coeficiente de x^5 del numerador que has obtenido entre el coeficiente de grado 5 del denominador (que es 25)
Te sugiero estos vídeos.. Limite infinito entre infinito 01
Nos cuentas ¿ok? -
Hola a todos, me podrian dar una mano sobre como continuar el ejercicio? Les dejo lo que hice, espero que este bien. Muchas gracias
-
Una Cuidad B se encuentra a 30km de A en dirección Este, mientras que C se encuentra a 50 km en direccion N30°O. La linea recta entre B y C representa una carretera entre las dos cuidades, mientras que la linea intermitente entre A y esta carretera representa un camino que desea construirse.
Determine la longitud de la Carretera entre B y C
Determine cual va a ser la longitud del camino entre A y la carretera que une a B y C
(Debería tener dibujo pero, en mi guía no está)
Gracias :) -
Cordial saludo:
Resulta que me he enredado con la serie que aparece en la imagen. Me indicarían el método que debo seguir para concluir si la serie (IMAGEN ANEXA) es convergente o divergente, ya que he aplicado los distintos criterios (comparación, raíz, de la integral, de la razón), pero ninguno me hes útil.
Gracias.






_Thumb.jpg)

_Thumb.jpg)



_Thumb.jpg)



_Thumb.jpeg)