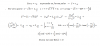-
Buenos dias ,no consigo encontrar la repuesta y por eso hago esta pregunta ,con el número 68373 cuantos número diferentes se pueden obtener y cuanto vale la suma de todos esos números ,a ver si alguien me puede resolver la duda ,no consigo dar con la fórmula para resolver este problema .Graciasaaa


Jose Ramos
el 25/1/20Como el 3 aparece dos veces, el total de números que se pueden formar son Permutaciones con repetición (el 3 dos veces, y los demás 1 vez) Sería RP52,1,1,1 = 5! / 2! = 60 números distintos
Para ver cuanto suman se hace lo siguiente:
Vemos cuantos acaban en 3 ( Fijo el 3 y me quedan 4 distintos para permutar) que son P4 = 4! = 24.
Acaban en 6 (Quedan 4 para permutar, pero el 3 aparece dos veces) son RP42,1,1 = 12
Acaban en 7 (igual que con 6) 12 y acaban en 8 otros 12.
Las unidades suman 3.24 + 6.12 +7.12+8.12 = 324. Llevamos 32 y sumamos las decenas: 324 + 32 = 356. Llevamos 35 y sumamos las centenas: 324 + 35 = 359
Llevamos 35 y sumamos los millares: 324 + 35 = 359. Llevamos 35 y sumamos las decenas de millar: 324 + 35 = 359.
La suma total es: 3.599.964
-


Jose Ramos
el 25/1/20Puedes hacerlo así: Estás buscando un plano π2 que pasa por el punto A(1,1,1) (Ya tenemos el punto). Ahora falta buscar dos vectores sobre el plano: uno de ellos es el vector director de la recta (-1,0,1) , pues la recta está contenida en el plano, al ser la intersección de π1 y π2.¿Dónde encontramos otro vector? ¡Fácil! Tomo un punto cualquiera de la recta, por ejemplo P (0,0,0) (en este caso) y hallo el vector PA = (1,1,1) que es (1,1,1). (Cuando sea así, asegúrate que los dos vectores que van a determinar el plano no sean proporcionales (dependientes), pues si no es así no determinan un plano).
-


Jose Ramos
el 25/1/20En efecto. Para ver que 3 puntos están alineados hay dos maneras de comprobarlo: Un es como hace el libro, es decir halla la recta que pasa por 2 de ellos y comprueba que el 3º está en dicha recta.
La otra forma es hallar los vectores AB y AC y comprobar que son dependientes (proporcionales) o el rango formando por ellos es 1.
-
Saludos gente del conocimiento y el saber xD
El proximo lunes tengo examen de ecuaciones diferenciales en la universidad. El problema es que hay un ejercicio que no me ha salido por nada del mundo el cual es:y'' - y = sec^3 (x) - sec(x)
Estaría eternamente agradecido
Gracias...


Breaking Vlad
el 27/1/20Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)