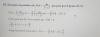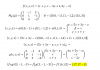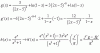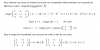-
Un comerciante sabe que 10 de cada 50 clientes que entran a su tienda a intentar robar los chicles. Una empresa de seguridad vende un software de deteccion de rostros y propone una prueba a los 5 primeros que entran, ofreciendo una licencia gratuita si comete algún error de predicción. Probabilidad de obtener licencia gratis?
Sería una binomial: X~b(n=5,p=0.2)
P(X>0)=1-P(0)=1-5C0*0.2^0*0.8^5?
-


Antonio Silvio Palmitano
el 28/12/198)
Vamos con una orientación.
Reemplazas las coordenadas del punto que es el único elemento del conjunto solución en las ecuaciones que tienes en tu enunciado, observa que en las dos primeras te quedan las Identidades Verdaderas: 5 = 5 y 3 = 3, respectivamente, y observa que en la tercera ecuación queda:
-2 + 0 - 3*a = a2, aquí cancelas el término nulo, restas a2 en ambos miembros, y queda:
-2 - 3*a - a2 = 0, multiplicas por -1 en todos los términos de esta ecuación, ordenas términos, y queda:
a2 + 3*a + 2 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
1°)
a = -1,
y para este valor tienes que al reemplazarlo en el sistema de ecuaciones de tu enunciado, éste queda compatible indeterminado y admite infinitas soluciones, en las que tienes que la solución única señalada en tu enunciado es una de las mismas (te dejo la tarea de resolver el sistema),
2°)
a = -2,
y para este valor tienes que al reemplazarlo en el sistema de ecuaciones de tu enunciado, éste queda compatible determinado y admite solución única, que es la que tienes indicada en tu enunciado.
Espero haberte ayudado.
-
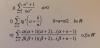 hola!! estos estudiando seris numericas, pero cuando hay parametros y
condiciones de mayor o menor, ya no se como se hacen, espero alguien me
pueda ayudar a explicarme como estudiar su caracter, saludos
hola!! estos estudiando seris numericas, pero cuando hay parametros y
condiciones de mayor o menor, ya no se como se hacen, espero alguien me
pueda ayudar a explicarme como estudiar su caracter, saludos

Antonio Silvio Palmitano
el 28/12/19Vamos con una orientación para los dos primeros.
j)
Observa que tienes una serie infinita de términos positivos, por lo que planteas la expresión del término general, y queda:
an = (n2+1)/(n*an) = n2(1+1/n2)/(n*an) = simplificas = n*(1+1/n2)/an;
luego, planteas la expresión del término general siguiente, y queda:
an+1 = ([n+1]2+1)/([n+1]*an+1) = (n2+2n+2)/([n+1]*an*a) = n2*(1+2/n+2/n2)/(n*[1+1/n]*an*a) = simplificas = n*(1+2/n+2/n2)/([1+1/n]*an*a);
luego, planteas la razón del término general siguiente entre el término general, y queda:
an+1/an = sustituyes expresiones = ( n*(1+2/n+2/n2)/([1+1/n]*an*a) ) / ( n(1+1/n2)/an ) = simplificas = ( (1+2/n+2/n2)/([1+1/n]*a) ) / (1+1/n2) =
resuelves la división entre expresiones, y queda:
= (1+2/n+2/n2) / ( (1+1/n2)*[1+1/n]*a );
luego, planteas el límite para n tendiendo a +infinito de la razón que tienes planteada, y queda:
Lím(n→+∞) [ an+1/an ] = sustituyes = Lím(n→+∞) [ (1+2/n+2/n2) / ( (1+1/n2)*[1+1/n]*a ) ] = resuelves = 1/( 1*a) = 1/a;
luego, de acuerdo con el Criterio de la Razón (o del Cociente), tienes tres opciones:
1°)
si 1/a < 1, que conduce a (recuerda que a es estrictamente positivo): a > 1, entonces tienes que la serie es convergente;
2°)
si 1/a > 1, que conduce a: a < 1, entonces tienes que la serie es divergente;
3°)
si 1/a = 1, que conduce a: a = 1, entones tienes que este criterio no decide,
por lo que reemplazas este valor en la expresión de la serie que tienes en tu enunciado, resuelves el denominador del término general, y queda:
∑(n=1,+∞) [ (n2+1)/n ] = ∑(n=1,+∞) [ n + 1/n ] = ∑(n=1,+∞) [ n ] + ∑(n=1,+∞) [ 1/n ],
que es la expresión de una serie divergente, ya que es igual a las suma de dos series divergentes cuyos términos son positivos.
Luego, puedes concluir que la serie de tu enunciado es:
a) convergente, si y solo si se cumple la condición: a > 1,
b) divergente, si y solo si se cumple la condición: 0 < a ≤ 1.
l)
Aquí prueba con el Criterio de la Raíz.
Haz el intento, y si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.