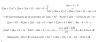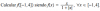logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    Osvaldo Pachacopa
    el 13/1/17
    flag

    Hola unicoos, me podrían ayudar con los siguiente ejercicio,desde ya gracias.... 



    reply•thumb_up•0 voto/s•flag
    icon

    David
    el 18/1/17

    Para el tercero.. Derivada enésima de una función

    Para el segundo y el primero... Dominio funcion irracional Dominio de una funcion

    Asintotas Crecimiento y curvatura  Continuidad de una función

    Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    poco
  • icon

    Raisa
    el 13/1/17

    Hola Unicoos,

    ¿Me ayudáis con éste ejercicio?

    Gracias!!!

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 13/1/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    jaime
    el 13/1/17

    Hola Unicoos, Me podéis ayudar con este ejercicio por favor


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 13/1/17


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Antonius Benedictus
    el 13/1/17


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Rosa
    el 13/1/17

     Hola Me podéis ayudar con este ejercicio por favor 

    en un anuncio dice pijamas antes 15,75 ahora11,95 zapatos antes 39,90ahora 29,95se quieres saber ¿si están rebajadas proporcionalmente? O si no es así ¿cuál lo es más?

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 13/1/17

    Puedes plantear las rebajas (R), y luego las rebajas porcentuales (Rp).

    Para los pijamas:

    R1 = 11,95 - 15,75 = -3,80, luego: Rp1 = (-3,80/15,75)*100 ≅ - 24,13 %.

    Para los zapatos:

    R2 = 29,95 - 39,90 = -9,95, luego: Rp2 = (-9,90/29,95)*100 ≅ -33,06 %.

    Observa que no están rebajadas proporcionalmente (los porcentajes de rebaja son distintos), y la mayor rebaja se dio en el precio de los zapatos.

    Observa que hemos planteado:

    Rebaja = Precio Nuevo - Precio Original

    Rebaja Porcentual = (Rebaja / Precio Original)*100.

    Espero haberte ayudado.




    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Rosa
    el 15/1/17

    Muchísimas gracias😄😄😄

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Raisa
    el 13/1/17

    Hola Unicoos,

    ¿Me ayudáis con éste ejercicio?

    Gracias!!!!


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 13/1/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Alejandro soto
    el 13/1/17
    flag

    Hola alguien me resuelve el 4.6.6  4.6.7 y el 4.6.8 por favor.

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 13/1/17

    Vamos con el ejercicio 466, y para resolverlo emplearemos el Método de los Multiplicadores de Lagrange.

    Observa que tienes una función f que es diferenciable en R3, cuyo gradiente queda expresado: ∇f = <1,1,1>.

    Observa que podemos considerar al elipsoide como una superficie de nivel de una función g que es diferenciable en R3, cuya expresión es: g(x,y,z) = x2 + 2y2 + 3z2, cuyo gradiente queda expresado: ∇g = <2x, 4y,6z>.

    Luego, planteamos el Sistema de Ecuaciones de Lagrange (indicamos con a al multiplicador real):

    1 = 2ax

    1 = 4ay

    1 = 6az

    x2 + 2y2 + 3z2 = 1

    Observa que las cuatro incógnitas no pueden tomar el valor cero porque no verificarían algunas de las cuatro ecuaciones (por ejemplo: si a = 0 o x = 0 no se veriicaría la primera ecuación), de ahí es que despejamos en las tres primeras ecuaciones:

    1 / 2a = x (1)

    1 / 4a = y (2)

    1 / 6a = z (3)

    luego sustituimos en la última ecuación resolvemos los cuadrados en los términos y queda:

    1 / 4a2 + 1 / 16a2 + 1 / 36a2 = 1, multiplicamos en todos los términos de la ecuación por 144 y queda:

    36/a2 + 9/a2 + 4/a2 = 144, resolvemos el primer miembro y queda:

    49/a2 = 144, hacemos pasajes de divisor como factor, de factor como divisor, y queda:

    49/144 = a2, hacemos pasaje de potencia como raíz y tenemos dos opciones:

    1) a1 = -7/12 ≠ 0, que al reemplazar en las ecuaciones señaladas (1) (2) (3) conduce a:

    x = -6/7, y = -3/7, z = - 2/7, o sea al punto de coordenadas: A(-6/7,-3/7,-2/7), para el que la función toma el valor: f(-6/7,-3/7,-2/7) = -11/7;
    2)     a2 = 7/12 ≠ 0, que al reemplazar en las ecuaciones señaladas (1) (2) (3) conduce a:

    x = 6/7, y = 3/7, z = 2/7, o sea al punto de coordenadas: A(6/7,3/7,2/7), para el que la función toma el valor: f(6/7,3/7,2/7) = 11/7.

    Luego, concluimos que la función alcanza un máximo absoluto en el punto A, y que alcanza un mínimo absoluto en el punto B.

    Espero haberte ayudado.



    thumb_up•2 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Antonio Silvio Palmitano
    el 13/1/17

    Vamos con el ejercicio 467. Observa que f es una función diferenciable (y por lo tanto también continua) en R2, restringida a un dominio que es cerrado y acotado, por lo que tenemos que la función f alcanza máximo absoluto y mínimo absoluto en el dominio, y solo nos falta determinar si estos extremos se encuentran en la región interior del dominio, o si se encuentran en su frontera, por lo que estudiaremos los dos casos por separado.

    Tienes la función cuya expresión es: f(x,y) = 2x2 - 3y2 - 2x, cuyo gradiente queda expresado: ∇f = <4x-2,-6y>.

    Luego, pasamos a estudiar:

    1) Región interior del dominio: Di = { (x,y) ∈ R2: x2 + y2 < 1 }.

    Planteamos la condición de punto estacionario (posible máximo o posible mínimo) para una función diferenciable (indicamos con N al vector nulo): ∇f = N, expresamos los vectores con sus componentes y queda: <4x-2,-6y> = <0,0>, luego, por igualdad entre vectores nos queda el sistema de ecuaciones:

    4x - 2 = 0, de aquí despejamos: x = 1/2

    - 6y = 0, de aquí despejamos: y = 0

    por lo que tenemos el punto de coordenadas: A(1/2,0) que pertenece a la región interior del dominio, por lo que lo consideramos como un punto crítico.

    2) Frontera del dominio: Df = { (x,y) ∈ R2: x2 + y2 = 1 }.

    Observa que la representación gráfica de la frontera del dominio es una circunferencia, a la que podemos considerar como una curva de nivel de la función g, diferenciable en R2, cuya expresión es: g(x,y) = x2 + y2, cuyo vector gradiente queda expresado: ∇g = <2x,2y>, luego planteamos el Sistema de Ecuaciones de Lagrange (indicamos con a al multiplicador real):

    4x - 2 = 2ax

    - 6y = 2ay

    x2 + y2 = 1

    Hacemos pasaje de término en la segunda ecuación y queda:

    -2ay - 6y = 0, extraemos factor común y queda:

    -2y(a + 3) = 0, luego, por anulación de un producto tenemos dos opciones:

    2a) -2y = 0, hacemos pasaje de factor como divisor y queda:

     y = 0, reemplazamos en las demás ecuaciones y queda:

    4x - 2 = 2ax

    x2 = 1, de aquí despejamos y tenemos dos opciones:

    2a1) x = -1, que al reemplazar en la otra ecuación y resolverla queda: a = 3, por lo que tenemos el punto de coordenadas: B(-1,0);

    2a2) x = 1, que al reemplazar en la otra ecuación y resolverla queda: a = 1, por lo que tenemos el punto de coordenadas: C(1,0).

    2b) a + 3 = 0, de donde despejamos:

    a = -3, reemplazamos en las demás ecuaciones y queda:

    4x - 2 = - 6x, de aquí podemos despejar: x = 1/5

    x2 + y2 = 1

    luego reemplazamos en la última ecuación, resolvemos el término cuadrático numérico y queda:

    1/25 + y2 = 1, hacemos pasaje de término y queda:

    y2 = 24/25, que nos conduce a dos opciones:

    2b1) y = -√(24/25), por lo que tenemos el punto de coordenadas: D( 1/5,-√(24/25) );

    2b2) y = √(24/25), por lo que tenemos el punto de coordenadas: E( 1/5,√(24/25) ).

    Y para terminar, solo queda que evalúes la función en los puntos críticos A, B, C, D y E, para ver en cuáles de ellos la función alcanza un valor máximo absoluto y en cuáles de ellos alcanza un valor mínimo absoluto.

    Espero haberte ayudado.




    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Alejandro soto
    el 13/1/17

    Muchas gracias.

    Solo una duda, al aplicar multiplicadores de lagrange lo que hay que hacer no es hacer las parciales (incluido el parámetro) de la función de lagrange y luego esas parciales igualarlas a 0 para hallar el punto critico??  Después ya se sustituye y se ve si es máximo... es que por mi forma que queda los puntos: A(1,1/2,1/3) máximo y B(-1,-1/2,-1/3) mínimo

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Antonio Silvio Palmitano
    el 13/1/17

    Si, Alejandro, es correcto tu planteo. Será cuestión de verificar cálculos, por las dudas se hayan deslizado errores, que pueden ser tanto tuyos como nuestros (el mar de ecuaciones y números muchas veces está revuelto), y en las dos formas de plantear debemos llegar a los mismos puntos críticos.

    Para el ejercicio 468, vamos con una orientación.

    El planteo y la resolución es muy similar a la que vimos en el ejercicio 467, nada más que extendido a R3.

    Haz el intento de resolver el ejercicio, y si te es necesario no dudes en volver a consultar.

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Alejandro soto
    el 13/1/17

    Perfecto creo que lo entiendo. Gracias por tu tiempo

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Bet
    el 13/1/17


    Buenas ¿Cómo se saca el valor esperado? ¿Qué es?


    reply•thumb_up•0 voto/s•flag
    icon

    Desencadenado
    el 13/1/17
    flag

    Suma los valores de la fila de abajo

    Respuesta e)1


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    poco
    icon

    Bet
    el 13/1/17

    Disculpa, la clave dice A) 
    :(

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Ángel
    el 13/1/17

    ∑15 P(X=xi)*X = (0.3*1)+(0.1*2)+(0.3*3)+(0.2*4)+(0.1*5)= 0.3+0.2+0.9+0.8+0.5= 2.7


    (( cuando pongo ∑15 me refiero al sumatorio entre 1 y 5, que son los valores mínimo y máximo que puede tomar i en xi  )) 


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Fredy
    el 13/1/17

    Hola, Por favor ayudarme con este ejercicio

    A una reunión empresarial en un conocido Salón de conferencias,
    asistieron 69 invitados  de los cuales
    10  tienen nacionalidad peruana y
    ecuatoriana; el número de invitados que son de nacionalidad peruana es igual al
    doble de los que sólo tienen nacionalidad ecuatoriana; y el número de invitados
    que no tienen nacionalidad peruana ni 
    ecuatoriana  es igual al triple de
    los que sólo tienen nacionalidad peruana.

    a.      
    Muestre en un diagrama de Venn la información
    dada y luego determine, ¿cuántos invitados sólo tienen nacionalidad ecuatoriana?                                



    ¿Qué porcentaje de los que tienen nacionalidad
    peruana representan los que tienen ambas nacionalidades?      

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 13/1/17


    thumb_up•3 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Antonius Benedictus
    el 13/1/17


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
  • icon

    Bet
    el 13/1/17


    reply•thumb_up•0 voto/s•flag
    icon

    Desencadenado
    el 13/1/17

    P(A)=0,35

    P(B)=0,3

    P(A∩B)=0,15

    0,35+0,3-0,15=0,5

    respuesta c)

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Desencadenado
    el 13/1/17

    Probabilidad LEY DE MORGAN

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Desencadenado
    el 13/1/17

    Probabilidad LEY DE MORGAN

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Carla
    el 13/1/17

    ¿pueden ayudarme con este?

    muchas gracias.

    reply•thumb_up•1 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 13/1/17

    Observa que, de acuerdo con la definición de valor absoluto, la expresión de la función queda en dos trozos:

    f(x) =

    x/(1-x)          si x ∈ [-1,0)

    x/(1+x)        si x ∈ [0,4]

    luego, observemos las expresiones:

    x/(1-x) = ( (x-1)+1 )/(1-x) = (x-1)/(1-x) + 1/(1-x) = - 1 + 1/(1-x),

    x/(1+x) = ( (1+x)-1)/(1+x) = (1+x)/(1+x) - 1/(1+x) = 1 - 1/(1+x);

    luego, la expresión de la función queda: 

    f(x) =

    -1 +1/(1-x)            si x ∈ [-1,0), observa que la expresión de la derivada para este trozo es: 1/(1-x)2 > 0 en todo el intervalo, por lo que este trozo es estrictamente creciente,

     1 - 1/(1+x)           si x ∈ [0,4], observa que la expresión de la derivada para este trozo es: 1/(1+x)2 > 0 en todo el intervalo, por lo que este trozo es estrictamente creciente.

    Luego, como el primer trozo es monótono creciente, evaluamos:

    f(-1) = -1 + 1/2 = - 1/2, y Lím(x→0-) ( -1 + 1/(1-x) ) = 0, por lo que tenemos: f( [-1,0) ) = [-1/2,0).

    Luego, como el segundo trozo es monótono creciente, evaluamos:

    f(0) = 1 - 1 = 0, f(4) = 1 - 1/4 = 4/5, por lo que tenemos: f( [0,4] ) = [0,4/5].

    Por último, planteamos:

    f( [-1,4] ) = f( [-1,0) ) u f( [0,4] ) = [-1/2,0) u [0,4/5] = [-1/2,4/5].

    Espero haberte ayudado.





    thumb_up•2 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Carla
    el 13/1/17

    muuuuchas gracias

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?