-
Tengo una intregral(x+3)^2 la puedo resolver aplicando la formula q dice q una f^n x su derivada es igual f^n+1\n+1. Me podrian aclarar esto????
-


Antonio Silvio Palmitano
el 4/8/16Una manera de designar a los números naturales impares es: x = 2n +1, con n>= 0, n es un número natural.
El siguiente número natural impar es igual a: y = 2n +1 +2 = 2n + 3.
Luego, a partir del enunciado tenemos:
x^2 + y^2 = 1570
reemplazamos y queda.
(2n + 1)^2 + (2n + 3)^2 = 1570
desarrollamos los binomios elevados al cuadrado y queda:
4 * n^2 + 4n + 1 + 4 * n^2 + 12n + 9 = 1570
reducimos términos semejantes y queda:
8 * n^2 + 16n + 10 = 1570
hacemos pasaje de término y reducimos, y llegamos a la ecuación:
8 * n^2 + 16n - 1560 = 0
dividimos en todos los términos por 8 y queda:
n^2 + 2n - 195 = 0
que es una ecuación polinómica cuadrática cuyas soluciones son:
n1 = -15 que no es un número natural, por lo tanto no es de interés para este ejercicio,
n2 = 13 que pertenece al conjunto de los números naturales, y a partir de ella tenemos que los números naturales son:
x = 2*13 +1 = 26 + 1 = 27
y = 2*13 + 3 = 26 + 3 = 29 (observa que 27^2 + 29^2 = 1570, por lo que se verifica la relación del enunciado)
y el siguiente número natural impar es:
z = 29 + 2 =31.
Espero haberte ayudado. -
Tengo que veriguar el area entre estas dos fuciones:
Y= senx
Y= -cosx
y dice en (0;pi) pero si se refiere a x=0 e y=pi entonces como hago? se refiere desde cero hasta pi? porque si se refiere al punto (0;pi) no le encuentro sentido
-


Antonio Silvio Palmitano
el 4/8/16Debes tener en cuenta que para calcular valores de relaciones trigonométricas puedes sumar o restar múltiplos enteros de un giro (1 giro = 360°).
Tenemos entonces:
a) sen(37*360° - 30°) = sen(37*360° - 30° - 37*360°) = sen(-30°) = -sen(30°) = -1/2 (por identidad trigonométrica en la anteúltima igualdad)
b) cos(-5*360° + 120°) = cos(-5*360° + 120° + 5*360°) = cos(120°) = -1/2 (por reducción del segundo al primer cuadrante)
Con los otros dos puedes proceder en la misma forma.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 4/8/16Aplicamos la misma idea del ejercicio de más arriba, veamos como ejemplo el ejercicio d), en el que tenemos a = 3895°:
primero observa que podemos restar diez giros completos, y queda:
a1 = 3895° - 10*360° = 3895° - 3600° = 295° que pertenece al intervalo [0 , 360°)
luego podemos restar un giro adicional y queda:
a2 = 295° - 360° = -65° que pertenece al intervalo (-180° , 180°]
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 4/8/16Observa que puedes multiplicar en todos los términos por 12, que es el Mínimo Común Múltiplo entre los tres denominadores, lo haces y la ecuación queda:
-2(2x - 1) +3(5x - 2) = 6(x- 1)
luego puedes distribuir en cada término y queda:
-4x + 2 + 15x - 6 = 6x - 6
luego reduces términos semejantes en el primer miembro y queda:
11x - 4 = 6x - 6
luego haces pasaje de términos y queda:
11x - 6x = -6 + 4
luego reduces términos semejantes y queda:
5x = -2
y por último haces un pasaje de factor como divisor y llegas a:
x = -2/5.
Es muy conveniente verificar la validez de la solución reemplazando este resultado en la ecuación original.
Espero haberte ayudado. -
Hola, que tal?
tengo un ejercicio de un examen final que no me sale, es una integral impropia entre 0 y +∞ de e∧(α²-4)x
Hay que verificar α tal que esa integral sea convergente.
si me pueden responder se los agradecería muchísimo ya que el lunes rindo y tengo esta duda. muchas gracias

Antonio Silvio Palmitano
el 4/8/16Observa que la integral impropia entre 0 y +inf de e^(-x) es convergente, y en general ocurre lo mismo con e^(kx), con k < 0.
Por lo tanto, una condición es_
a^2 - 4 < 0
luego
a^2 < 4
luego
|a| < V(4)
|a| < 2
y concluimos:
-2 < a < 2.
Luego, solo queda resolver la integral impropia.
Espero haberte ayudado. -


Antonio Silvio Palmitano
el 4/8/16Puedes reescribir la ecuación, a partir de la propiedad de una potencia cuya base es otra potencia en el primer término:
(3^x)^2 - 3^x - 6 = 0
luego la sustitución: w = 3^x, reemplazas y queda:
w^2 - w - 6 = 0
que es una ecuación polinómica cuadrática, cuyas soluciones son: w1 = -2, w2 = 3
a) para w1 = -2 tenemos:
3^x = -2 que es absurda, porque la función exponencial siempre toma valores reales estrictamente positivos
b) para w2 = 3 tenemos:
3^x = 3
3^x = 3^1
x = 1.
Espero haberte ayudado.




_Thumb.jpg)

_Thumb.jpg)




_Thumb.jpg)


_Thumb.jpg)


_Thumb.jpg)
_Thumb.png)
_Thumb.jpg)

_Thumb.jpg)





_Thumb.jpg)

_Thumb.jpg)

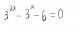

_Thumb.jpg)
