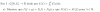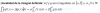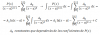-
 Jose Ramos ,gracias por tu enorme ayudo,si me acuerdo que me dijiste que se podia calcular el area ,pero dijiste mediante un trapecio rectangulo y no entendi como ,yo lo resolvi usando el triangulo rectangulo(sabiendo que k es -1/2)
Jose Ramos ,gracias por tu enorme ayudo,si me acuerdo que me dijiste que se podia calcular el area ,pero dijiste mediante un trapecio rectangulo y no entendi como ,yo lo resolvi usando el triangulo rectangulo(sabiendo que k es -1/2)
pero no me dio el resultado ya que 3 por 1, dividido en 2 es 1,5 y deberia dar uno,pero como se graficaria mediante el trapecio rectangulo?no entiendo eso,de antemano graciass¡
-
-
buenas, quisiera saber el ¿por qué? las funciones sen(x) y cos(x) tienen infinitas raíces; siendo así ¿porque también en la calculadora al sacar la raíz de esta función sin haberle adicionado valores a "x" siempre arroja una sola solución "me parece curioso pero he encontrado muy poca información"; agradezco su ayuda.
-


Antonio Silvio Palmitano
el 27/12/19Vamos con una orientación.
Puedes plantear el Desarrollo de Taylor del polinomio cuya expresión tienes en el numerador del argumento de la integral, alrededor del centro de desarrollo: x0 = a, y observa que te quedará una suma de potencias del binomio: (x - a); luego, puedes distribuir el denominador entre todos los términos del desarrollo, y luego integrar término a término.
Observa que la expresión general del polinomio es:
Pn(x) = ∑(k=0,n) ak*xk, cuyo desarrollo de Taylor queda:
Pn(x) = ∑(k=0,n) [P(k)(a)/k!]*(x - a)k, que al desarrollar la suma, queda:
Pn(x) = P(0)(a) + P(1)(a)*(x - a) + [P(2)(a)/2!]*(x - a)2 + [P(3)(a)/3!]*(x - a)3 + ... + [P(n)(a)/n!]*(x - a)n,
y observa que al dividir en todos los términos por (x - a)n+1, queda:
Pn(x) / (x - a)n+1 = P(0)(a)/(x - a)n+1 + P(1)(a)*(x - a)/(x - a)n+1 + [P(2)(a)/2!]*(x - a)2/(x - a)n+1 + [P(3)(a)/3!]*(x - a)3/(x - a)n+1 + ... + [P(n)(a)/n!]*(x - a)n/(x - a)n+1,
y al simplificar en todos los términos a partir del segundo de ellos, queda:
Pn(x) / (x - a)n+1 = P(0)(a)/(x - a)n+1 + P(1)(a)/(x - a)n + [P(2)(a)/2!]/(x - a)n-1 + [P(3)(a)/3!]/(x - a)n-2 + ... + [P(n)(a)/n!]/(x - a),
y luego puedes integrar término a término,
y queda para ti plantear las expresiones de las derivadas del polinomio, y evaluarlas para el centro de desarrollo.
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Gracias Antonio por tu respuesta!!!
Tú me enviaste:
Cambiamos entonces:como log3(4-2) = log3(2)
y log3(4) = log3(22) = 2*log3(2)
tenemos que:
log3(4) / log3(4-2) = 2*log3(2) / log3(2) = ...
simplificando
... = 2
Por lo tanto tenemos que: log3(4) / log3(4-2) = 2
Este es el primer término de una ecuación log
Uniendo lo que tu me enviaste al numerador quedaría así, como está en la foto?
Desde ya muchísimas gracias! -

Antonio
el 27/12/19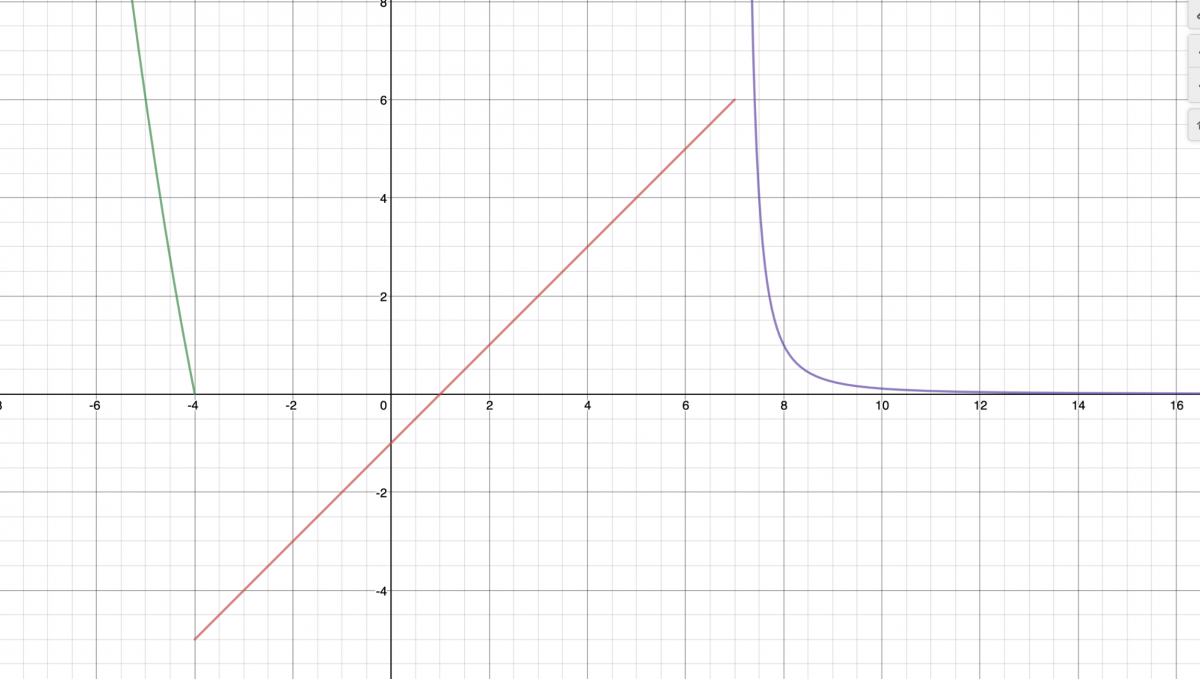
La función no es continua en x=-4 pues no existe el límite de la función en x=-4 pues el límite por la izquierda es 0 y por la derecha -5
La función no es continua en x=7 pues no existe el límite de la función en x=7 pues el límite por la izquierda es 6 y por la derecha más infinito
Para el resto de puntos la función es continua, ya que en los dos primeros trozos es función polinómica y en el tercero es el cociente de dos funciones continuas donde el denominador no se anula (en el intervalo)
por lo tanto:
f(x) es continua en ℛ-{-4,7}
presentando en x=-4 una discontinuidad de primera especie de salto finito
y en x=7 una discontinuidad de primera especie de salto infinito