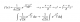-
Mientras repasando para un global de matematicas en un video de optimizacion de David, explico que se puede realizar la integral de una division subiendo el denominador con exponente y resolviendolo (uso f(x)=2/R). por tanto intente este metodo con una funcion un pelin mas compleja y el resultado me sale correcto. Este metodo me resulta mucho mas corto que la formula f(x)/g(x)=(f'(x)*g(x)-f(x)*g'(x))/(g(x))^2. Mi pregunta es si este metodo siempre resulta mas rapido o hay casos donde se convierte en una ecuacion muy compleja? cuando aconsejarias usarla? Existen casos donde este metodo no funciona? Graciass
-
Hola!
Me podrían resolver una función de examen de uned del 2015 modelo3 -pregunta 3 opción A .gracias -
Hola buenas, me podrían decir si esta integral définida está bien realizada? Es que en las soluciones pone otra cosa, y creo que mi error se encuentra en haber sacado un -2 en lugar de la constante entera -8, pero lo he hecho para obtener la derivada de la función de abajo. Sin embargo no se hace así, no se podría hacer eso?
-
Hola maestros de unicoos, saludos, me podrian hechar una manita con una integral que da vueltas y vueltas.
∫ (4 Csc x Cotx +2 Sec²x) dx
No se como hacer, por el método normal o sustitución ya que ese 4 cosecante por cotangente de la variable me complica la vida.
Gracias de antemano maestros unicoos.
Saludos
Att: El Toby -
Buenas noches como puedo empezar esta integral , estaba resolviendo con una sustitucion pero luego de resolver todo me queda en infinito :(... me pueden guiar por favor gracias de antemano.
-
Si f(x)=g(x) en el intervalo -o.oo1< x < 0.0001 entonces, lim f(x) = 3 cuando x___> 0 eso implica lim g(x) = 3 cuando x____> 0 .Tengo que justificarlo analizando la veracidad Mi duda como tengo que encararlo partiendo con la 1° funcion f(x) vale 3 ? que se cumple los lim laterales? y valen lo mismo? o por la unicidad del limite. Espero alguna respuesta Gracias
-
esto es muy urgente ayuda
Decimos que una matriz A cuadrada es ortogonal, si y sólo si, las
columnas de la matriz son vectores unitarios y ortogonales entre
si. Decida si cada una de las siguientes proposiciones es falsa o
verdadera y diga por qué.
a) Si A es una matriz ortogonal, entonces ATA = I.
b) Toda matriz ortogonal es invertible.
c) Si A es una matriz ortogonal, AT
también es ortogonal.
d) La matriz idéntica es ortogonal.
e) La inversa de una matriz ortogonal es su transpuesta.
f ) Si A es una matriz ortogonal, la solución del sistema de ecuaciones
lineales Ax = b es x = ATb. -
-
Hola unicoos! podrían decirme si este problema se puede resolver con casquillos? y cual sería el resultado, yo obtuve 42.41




_Thumb.jpg)





_Thumb.jpg)


_Thumb.jpg)
_Thumb.png)

_Thumb.jpg)




_Thumb.jpg)