-
Hola, necesito que me ayuden a resolver esta derivada por favor.
Es un ejercicio que encontré en vitutor.com, pero no entiendo como llegaron al resultado.
Lo que yo haría seria aplicar la propiedad de la raiz, por lo tanto el numerados me quedaría como una raiz cubica y tambien el denominador. Luego aplicaría la propiedad de la derivacion de una division que es {(u'*v)-(u*v')}/2 Pero en vitutor me aparece otra cosa, por lo tanto me confundo.
Agradecería su respuesta. muchas gracias -
Hola, necesito ayuda con estos 3 ejercicios. El primero me tiene que dar raiz de dos entre 4 y eso me dio, pero no se si mi procedimiento este correcto ya que no estoy segura de que se le pueda cambiar el signo a la raiz. El segundo no se como resolverlo, no se si aplicar ln ya que al aplicarlo me da algo raro...El tercero, Lo hice pero tampoco se si este bien...
-


David
el 5/5/16La altura viene dada por la funcion... En el apartado a) simplemente tienes que igualar la funcion a 25... Te quedará 25=-16t²+30t+60...
En el b), se trata de hallar el vertice de la funcion y=-16t²+30t+60... Representacion funcion cuadratica -
buenas noches alguien me podria ayudar con estos ejercicios necesito encontrar el rango de estas funciones:
a)y=2-ke^{-cos(x)}, donde k = 2 y k = -2
c) y = (3pi/2)+2kpi-x, donde k = 2 y k = -2
porfa -
Hola buenas noches creen que me ayudan o al menos un video que se entienda bien eso, la verdad no le entiendo al 9 mas que todo, y lo necesito y no lo puedo hacer, me ayudarian porfa

lilith
el 3/5/16las dimensiones son
a)4
b) 1 por que al hacer combinacion lineal tienes {(1,0,0)+(0,x,0)+(0,0,x^{2})} = {(1,0,0)+x(0,1,0)+x^{2}(0,0,1)}, donde x pertenece a los reales.
c)4
para las bases ortonormales la u1=(1,1,0)
u2=(0,1,1)-{<(0,1,1)(1,1,0)>/||(1,1,0)||^{2} }(1,1,0)
u2=(0,1,1)-{1/||raiz(2)||^{2} }(1,1,0)
u2=(0,1,1)-{1/2}(1,1,0) = (0,1,1)+(-1/2,-1/2,0) = (-1/2,1/2,1)
u3=(1,0,1)-{<(1,0,1)(1,1,0)>/||(1,1,0)||^{2} }(1,1,0)-{<(1,0,1)(0,1,1)>/||(0,1,1)||^{2} }(0,1,1)
u3=(1,0,1)-{1/||raiz(2)||^{2} }(1,1,0)-{1/||raiz(2)||^{2} }(0,1,1)
u3=(1,0,1)-{1/2}(1,1,0)-{1/2 }(0,1,1)
u3=(1,0,1)+(-1/2,-1/2,0)+(0,-1/2,-1/2)
u3=(1/2,-1/2,1)+(0,-1/2,-1/2)= (1/2,-1,1/2)
u={(1,1,0),(0,-1/2,-1/2), (1/2,-1,1/2)}



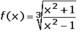






_Thumb.jpg)
_Thumb.jpg)

_Thumb.jpg)




_Thumb.jpg)


